Пусть задан треугольник с катетами a и b и гипотенузой c. Высота h = 21 опущена из вершины С на гипотенузу с, а угол А = 60°. Второй острый угол этого прямоугольного треугольника равен ∠В = 90° - 60° = 30°. Больший катет всегда лежит против большего угла, поэтому большим катетом является катет а, лежащий против большего угла А. Рассмотрим прямоугольный треугольник, образованный большим катетом a заданного треугольника, высотой h, опущенной на гипотенузу и проекцией большего катета a на гипотенузу.
В этом треугольнике гипотенузой является больший катет a заданного треугольника, а высота h = 21 является катетом, лежащим против ∠В = 30° . Известно, что катет, лежащий против угла в 30°, равен половине гипотенузы. Поэтому b = 2h = 2 · 21 = 42.
42.
Объяснение:
Пусть задан треугольник с катетами a и b и гипотенузой c. Высота h = 21 опущена из вершины С на гипотенузу с, а угол А = 60°. Второй острый угол этого прямоугольного треугольника равен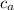 большего катета a на гипотенузу.
большего катета a на гипотенузу.
∠В = 90° - 60° = 30°. Больший катет всегда лежит против большего угла, поэтому большим катетом является катет а, лежащий против большего угла А.
Рассмотрим прямоугольный треугольник, образованный большим катетом a заданного треугольника, высотой h, опущенной на гипотенузу и проекцией
В этом треугольнике гипотенузой является больший катет a заданного треугольника, а высота h = 21 является катетом, лежащим против ∠В = 30° .
Известно, что катет, лежащий против угла в 30°, равен половине гипотенузы. Поэтому b = 2h = 2 · 21 = 42.