Основою прямої призми є рівнобедрений трикутник з основою 8 см і висотою, проведеної до неї завдовжки 3см. Знайдіть площу бічної поверхні, якщо її висота дорівнює 6см. [RUS] Основой прямой призмы является равнобедренный треугольник с основанием 8 см и высотой, проведенной к ней длиной 3 см. Найдите площадь боковой поверхности, если ее высота равна 6 см.
Объяснение:
Так как призма прямая, то длина ее высоты равна длине бокового ребра призмы.
Площадь боковой поверхности призмы равна:
S(бок) = S(AA₁C₁C) + S(BB₁C₁C) + S(AA₁B₁B)
Найдем боковую сторону равнобедренного треугольника в основании призмы:
Проведем высоту BH равнобедренного треугольника ABC с основанием AC.
По свойству высоты равнобедренного треугольника, проведенной к основанию, BH будет медианой, поэтому AH = CH = AC/2 = 4 см
По теореме Пифагора найдем AB:
AB =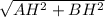 =
= 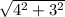 = 5
= 5
S(AA₁C₁C) = AA₁ * AC = 6 * 8 = 48 см²
S(BB₁C₁C) = BB₁ * BC = 6 * 5 = 30 см²
S(AA₁B₁B) = AB * AA₁ = 5 * 6 = 30 см²
S(бок) = 48 см² + 30 см² + 30 см² = 108 см²