1) Площадь правильного треугольника может быть вычислена по формуле:
откуда (для удобства вычислений все величины будем пока оставлять в
квадрате):
Но следует при этом помнить, что квадрат половины боковой стороны равен:
Квадрат апофемы боковой грани равен:
Квадрат половины расстояния между двумя противоположными вершинами
октаэдра равен:
Расстояние между двумя противоположными вершинами октаэдра равно:
см
2) Углом между прямой и плоскостью называется меньший из углов между прямой и
еёпроекцией на плоскость. В данном случае это будет угол СВК. Поскольку ребром
правильного тетраэдра является правильный (равносторонний) треугольник (в
котором все углы равны и составляют 60⁰), то его медиана ВК является также
биссектрисой и высотой. Из этого следует, что искомый угол равен 30⁰
Не забудь отметить как "Лучшее решение", ОК?!.. ;)))
Элементарно, Ватсон! ;)
Как известно, ромб обладает следующим замечательными свойствами, которые мы применим при решении данной задачи:
"Площадь ромба равна половине произведения его диагоналей"
"Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам"
Отсюда следует что площадь ромба равна:
см²
Длина стороны ромба равна:
Поскольку площадь одной боковой грани равна:
находим высоту призмы :
Объём призмы, таким образом равен:
Как "Лучшее решение" отметить не забудь, ОК?!.. ;)))
1) Площадь правильного треугольника может быть вычислена по формуле:
откуда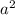 (для удобства вычислений все величины будем пока оставлять в
(для удобства вычислений все величины будем пока оставлять в
квадрате):
Но следует при этом помнить, что квадрат половины боковой стороны равен:
Квадрат апофемы боковой грани равен:
Квадрат половины расстояния между двумя противоположными вершинами
октаэдра равен:
Расстояние между двумя противоположными вершинами октаэдра равно:
2) Углом между прямой и плоскостью называется меньший из углов между прямой и
еёпроекцией на плоскость. В данном случае это будет угол СВК. Поскольку ребром
правильного тетраэдра является правильный (равносторонний) треугольник (в
котором все углы равны и составляют 60⁰), то его медиана ВК является также
биссектрисой и высотой. Из этого следует, что искомый угол равен 30⁰
Не забудь отметить как "Лучшее решение", ОК?!.. ;)))
Элементарно, Ватсон! ;)
Как известно, ромб обладает следующим замечательными свойствами, которые мы применим при решении данной задачи:
"Площадь ромба равна половине произведения его диагоналей"
"Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам"
Отсюда следует что площадь ромба равна:
Длина стороны ромба равна:
Поскольку площадь одной боковой грани равна:
Объём призмы, таким образом равен:
Как "Лучшее решение" отметить не забудь, ОК?!.. ;)))