Основания трапеции относятся как 3:11, а одна из диагоналей равна 42 см. Найдите отрезки, на которые делит эту диагональ вторая диагональ трапеции.
3. В окружности хорда, перпендикулярная диаметру. делит его на отрезки 5 см и 45 см. Найдите длину хорды. (ВСЕ ЗАДАНИЯ ЖЕЛАТЕЛЬНО С ЧЕРТЕЖОМ, ПЛЗ)

Показать ответ

Ответ:

olgagolikova2

06.10.2022 01:33

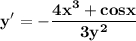
1. $\displaystyle \bf y'=-\frac{4x^3+cosx}{3y^2}$

2. $\displaystyle \bf y'(x)=-\frac{2}{t^2cost}$

3. $\displaystyle \bf y_k=-0,06x+0,72$ ;

$\displaystyle \bf y_n=\frac{50}{3}x+50,9$ .

Объяснение:

1. Найти производную функции у(х), которая задана неявно уравнением:

$\displaystyle x^4+y^3+sinx=0$

Так как у является функцией от х, то будем рассматривать у³ как сложную функцию от х.

$\displaystyle 4x^3+3y^2\cdot y'+cosx=03y^2\cdot y'=-4x^3-cosxy'=\frac{-4x^3-cosx}{3y^2}$

$\displaystyle \bf y'=-\frac{4x^3+cosx}{3y^2}$

2. Найдите производную функции y (x), заданную параметрически.

$\displaystyle \left \{ {{x=sint} \atop {y=\frac{2}{t} }} \right.$

Формула производной для функции, заданной параметрически:

$\boxed {\displaystyle \bf y'(x)=\frac{y'(t)}{x'(t)} }$

Найдем x'(t) и y'(t):

$\displaystyle x'(t)=cost\\ \\ y'(t)=-\frac{2}{t^2}$

$\displaystyle \bf y'(x)=-\frac{2}{t^2cost}$

3. Найти уравнение касательной и нормали к графику функции y= f(x) в точке абсциссой x₀.

$\displaystyle y=\frac{x^2}{x^2+1} ,\;\;\;\;\;x_0=-3$

Найдем производную:

$\displaystyle y'=\frac{(x^2)'\cdot (x^2+1)-x^2\vdot(x^2+1)'}{(x^2+1)^2} =\frac{2x\cdot(x^2+1)-x^2\cdot 2x}{(x^2+1)^2} ==\frac{2x^3+2x-2x^3}{(x^2+1)^2} =\frac{2x}{(x^2+1)^2}$

Найдем значение функции и ее производной в точке x₀ = -3.

$\displaystyle y(-3)=\frac{9}{9+1 }=\frac{9}{10}=0,9$

$\displaystyle y'(-3)=\frac{-6}{(9+1)^2}=-\frac{6}{100} =-0,06$

Уравнение касательной:

$\boxed {\displaystyle \bf y_k=y(x_0)+y'(x_0)(x-x_0)}$

$\displaystyle y_k=0,9+(-0,06)(x-(-3))=0,9-0,06(x+3)=\\ \\=0,9-0,06x-0,18=-0,06x+0,72$

Получили уравнение касательной:

$\displaystyle \bf y_k=-0,06x+0,72$

Уравнение нормали:

$\boxed {\displaystyle \bf y_n=y(x_0)-\frac{1}{y'(x_0)} (x-x_0)}$

$\displaystyle y_n=0,9-\frac{1}{-0,06} \cdot(x-(-3))=0,9+\frac{100}{6} (x+3)==0,9+\frac{50x}{3} +50=\frac{50}{3}x+50,9$

Получили уравнение нормали:

$\displaystyle \bf y_n=\frac{50}{3}x+50,9$

#SPJ1

0,0(0 оценок)

Ответ:

ладаседан7

14.12.2021 11:32

ответ: Координаты точки B (10;1).

Объяснение:

Точка А (2; 5) один из концов отрезка AB. Точка C (6; 3) - середина отрезка АВ Найди координаты точки В.

Дано: 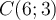$\large \boldsymbol {} A(2;5)$ , $\large \boldsymbol {} C(6;3)$ - середина отрезка АВ

Найти: $\large \boldsymbol {} B(x;y)$

Координата середины отрезка равна полусумме соответствующих координат его концов:

x = (x₁+x₂)/2 и y = (y₁+y₂)/2 ⇒ найдём другой конец отрезка АВ:

$\large \boldsymbol {} X_c=\frac{X_B+X_A}{2}$ $\large \boldsymbol {} Y_C=\frac{Y_B+Y_A}{2}$

$\large \boldsymbol {} 6 =\frac{X_B+2}{2}$ (домножим на 2) $\large \boldsymbol {} 3 = \frac{Y_B+5}{2}$ ( домножим на 2)

12 = X_B+2 6=Y_B+5

-X_B=2-12 -Y_B=5-6

-X_B=-10 -Y_B=-1

X_B=10 Y_B=1

Координаты точки B (10;1)

#SPJ1

0,0(0 оценок)

Популярные вопросы: Геометрия

Celovek21

26.05.2022 07:47

ПРОСНИСЬ КРОШКА ТЫ ПРОДАЕШЬСЯ ТЫ ПРОДАЕШЬСЯ...

tana29143Танечка

10.03.2021 04:52

через точку м находящуюся на расстоянии 18 от окружности с центром в точке о и радиусом 7 проведена прямая касающаяся этой окружности в точке к найдите расстояние от...

Motya232

08.04.2021 11:12

Дано AC дорівнює AD , BC дорівнює BD кут C дорівнює 102° знайти кут D...

вообшетоямаг

16.10.2021 13:24

В прямоугольной трапеции основания равны 6см. и 9см., а большая боковая сторона равна 5см. Найти периметр трапеции....

dasharisk2104

12.07.2020 12:21

ВопросПериметр ромба 100 см, одна из его диагоналей 48 см. Найдите длину второй диагонали ромба.ответ дайте без единиц измерений....

Ответит7275

12.07.2021 17:07

ВопросДиагонали ромба 10 см и 24 см. Найдите длину стороны ромба. ответ дайте без единиц измерений....

mkalashnik1983

17.05.2023 00:45

правильный ответ. Упростите: векторОТ +вектора MK + векторPH + векторHM + векторТР -векторOK-векторОМ-векторОР-векторОН...

mail000alomer

03.08.2021 13:54

Найдите катет прямоугольного треугольника, если его гипотенуза равна 13 см и второй катет равен 5 м....

turkmenochka75

14.01.2023 22:38

Можно ответ в полном виде...

malina2017

22.03.2023 10:34

Знайдiть площу ортогональної проекцiї трикутника зi сторонами 7 см, 17 см i 18 см на площину, що утворює з площиною трикутника кут 45°....

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку