Основанием пирамиды dabcявляется правильный треугольник - вопрос №1608810 от sooooooyeees 28.03.2023 05:15

Question

Геометрия: Основанием пирамиды dabcявляется правильный треугольник авс, сторона которого равна a. ребро da перпендикулярно к плоскости авс, а плоскость dbc составляет с плоскостью авс угол 30о. найдите площадь боковой поверхности пирамиды. подробное решение . буду .

sooooooyeees · Answer

Пусть АН- высота основания пирамиды. Поскольку в основании- правильный треугольник, то его высоты являются и медианами, следовательно ВН=СН=а/2

Находим АН:

$AH=\sqrt{a^2-(\frac{a}{2})^2}=\sqrt{a^2-\frac{a^2}{4}}=\sqrt{\frac{4a^2-a^2}{4}}=\sqrt{\frac{3a^2}{4}}=\frac{a\sqrt{3}}{2}$

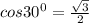Зная $cos30^0=\frac{\sqrt3}{2}$ , находим DH:

$DH=\frac{AH}{cos30^0}=\frac{a\sqrt3}{2}:\frac{\sqrt3}{2}=\frac{a\sqrt3}{2}\cdot\frac{2}{\sqrt3}=a$

Высота пирамиды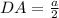 $DA=\frac{a}{2}$ , как катет, лежащий против угла в 30⁰

Теперь, зная все нужные значения, находим площадь боковой поверхности пирамиды:

$S_6_o_k=2\cdot\frac{a\cdot\frac{a}{2}}{2}+\frac{{a^2}}{2}=\frac{{a^2}}{2}+\frac{{a^2}}{2}=a^2$

Ну и, как "Лучшее решение" не забудь отметить, ОК?!... ;)))