Определи верность или неверность высказываний, представленных ниже. Если расстояние между центральными точками двух несовпадающих окружностей равно произведению их радиусов, то такие окружности имеют общую точку.
Опирающиеся на одну дугу вписанные углы в данной окружности равны.
Когда вписанный в окружность угол равен 45°, то дуга окружности, на которую опирается этот угол, будет равна 195°.
Через любые четыре точки, не принадлежащие одной прямой, проходит единственная окружность.
в равнобедренном треугольнике, высота проведённая к основанию, является медианой, поэтому основание делится на 2 равных отрезка по 5 см. По теореме Пифагора найдём боковую сторону
корень из 5^2+5^2= корень из25+25= корень из25*2=5 корень из2
найдём площадь треугольника, она равна половине произведения основания и высоты, поэтому S=1/2*a*h=1/2*10*5=5*5=25см^2
эту же площадь можно вычислить по другому
S=abc/4R, отсюда
R=abc/4S=10*5 корень из2*5 корень из2/4*25=10*25*2/100=5
эту же площадь можно вычислить как половина произведения периметра на радиус вписанной окружности S=1/2*P*r, r=2*S/P
P=10+2*5 корень из2=10+10 корень из2=10(1+ корень из 2)
r=2*25/10(1+ корень из 2)=5/(1+ корень из 2)=5*(1- корень из 2)/(1+ корень из 2)(1- корень из 2)=5( корень из 2-1)
Проведём от вершин верхнего основания высоты ВН иСМ
Дальше для простоты я обозначаю всё малыми буквами.
ΔАСМ прякоугольный, угол САМ=30⁰, значит
Из ΔАСМ по т. Пифагора находим АМ:
Из вершины А поднимем перпендикуляр до пересечения в точке О с продолжением основания ВС.
ΔАОВ=ΔСМD по равен по певому признаку равенства прямоугольных треугольников (по катету и гипотенузе; хотя там можно и больше признаков найти).
Значит получаем основное соотношение для решения задания:
Находим сумму оснований трапеции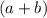
из соотношения:
Ну и, поскольку знаем, что
Средняя линия трапеции параллельна основаниям и равна их полусумме, то:
Как "Лучшее решение" отметить не забудь, ОК?!.. ;)))