Определи, какую силу надо приложить к свободному концу троса, перекинутого через блок 2, чтобы эластичный трос, перекинутый через неподвижный блок 1, был натянут с силой 4600 Н.
(Трением и весом блоков можно пренебречь).
ответ: к свободному концу троса надо приложить силу
кН.
Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Параллельные стороны трапеции ( BC и AD ) называются основаниями трапеции, а не параллельные ( AB и CD ) - боковыми сторонами. Перпендикуляр ( BH ), проведенный из любой точки одного основание к другому основанию или его продолжению называется высотой трапеции.
Теория: Четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны, называется трапецией. Параллельные стороны трапеции называются её основаниями. ... Трапеция, у которой одна боковая сторона перпендикулярна основаниям, называется прямоугольной трапецией.
Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией (реже равнобокой или равнобочной трапецией). Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Объяснение:
вроде все правильно
Дано: RSQT-трапеция , ∠SRK=∠QTK=45°,RE=ES=TF=FQ, SQ=10 ,SK=8, SK⊥RT. Найти: RT,EF.
Объяснение:
Т.к. RE=ES=TF=FQ ⇒ RS=TQ ⇒ RSQT- равнобедренная трапеция.
Для равнобедренной трапеции справедливо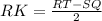
(*).
Из прямоугольного ΔRKS найдем RK : тк один из острых углов 45°, то и другой острый угол 45°⇒ ΔRKS- прямоугольный равнобедренный ⇒SK=RK=8. Получаем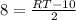
или RT=26 .
EF-средняя линия , т.к. по условию она проходит через середины сторон RS ,TQ ⇒ EF=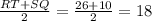
=================================
(*) Высота , опущенная из вершины на большее основание , делит его на большой отрезок , который равен полусумме оснований и меньший- равен полуразности оснований.