Обозначим центр малой окружности через . Если окружность касается хорды, то по свойствам касательной радиус окружности перпендикулярен хорде в этой точке: .
Если отрезок перпендикулярен хорде, то при их пересечении он делит хорду пополам (это теорема, которую изучают в школе). Значит, точка — середина хорды . Треугольник равнобедренный (поскольку отрезки и равны как радиусы). Значит, медиана является также и высотой. Получим, что . Учитывая предыдущее равенство, получим, что . Это значит, что точки и лежат на одной прямой. Тогда на той же прямой лежит точка касания (ведь по условию она диаметрально противополож
Треугольник с прямым углом - это прямоугольный треугольник.
Так как меньшие стороны "прилегают" к прямому углу, то эти стороны - катеты.
Так как катеты имеют длины 6 см и 8 см, то также такой треугольник - египетский (треугольник с соотношением сторон, равным 3:4:5). Следовательно, гипотенуза равна 10 см (можно также проверить через теорему Пифагора).
Высота, проведённая к большей стороне - высота, проведённая к гипотенузе (так как гипотенуза - самая большая сторона в прямоугольном треугольнике).
Высота, проведённая к гипотенузе равна произведению катетов, делённому на гипотенузу.
См. рисунок.
Обозначим центр малой окружности через
. Если окружность касается хорды, то по свойствам касательной радиус окружности перпендикулярен хорде в этой точке: 
.
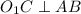Если отрезок перпендикулярен хорде, то при их пересечении он делит хорду пополам (это теорема, которую изучают в школе). Значит, точка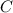
— середина хорды 
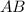. Треугольник 
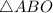равнобедренный (поскольку отрезк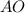и 
и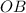 
равны как радиусы). Значит, медиана 
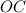является также и высотой. Получим, что 
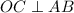. Учитывая предыдущее равенство, получим, что 
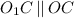. Это значит, что точки 
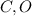и 
лежат на одной прямой. Тогда на той же прямой лежит точка касания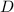 
(ведь по условию она диаметрально противополож
Треугольник с прямым углом - это прямоугольный треугольник.
Так как меньшие стороны "прилегают" к прямому углу, то эти стороны - катеты.
Так как катеты имеют длины 6 см и 8 см, то также такой треугольник - египетский (треугольник с соотношением сторон, равным 3:4:5). Следовательно, гипотенуза равна 10 см (можно также проверить через теорему Пифагора).
Высота, проведённая к большей стороне - высота, проведённая к гипотенузе (так как гипотенуза - самая большая сторона в прямоугольном треугольнике).
Высота, проведённая к гипотенузе равна произведению катетов, делённому на гипотенузу.
То есть -
h = 4,8 см.
ответ: 4,8 см.