Я решила так. 1. Правильный пятиугольник, сторона = 1 см. Отношение диагонали правильного пятиугольника к стороне = золотому сечению (то есть числу (1+√5)÷2). Считаем: х÷1 = (1+√5)÷2 x = 1.6180339888 (см)
2.Правильный шестиугольник, сторона = 5 см. При проведении меньшей диагонали получаем треугольник, у которого тупой угол = 120°, острые углы = по 30° каждый.
Решение 1. Меньшая диагональ правильного шестиугольника в √3 раз больше его стороны (это - свойство правильного шестиугольника), то есть = 5×√3 = 8.6602540378 (см).
Решение 2. Основано на правиле о том, что катет, лежащий против угла в 30°, равен половине гипотенузы. Нарисуй, и сразу все увидишь! Если провести в правильном шестиугольнике и меньшую, и большую диагонали, то большая диагональ является гипотенузой прямоугольного треугольника, а меньшая диагональ является одним из катетов. Получается, что нам именно и известен этот самый катет, лежащий напротив угла в 30°, он = 5 см. Тогда гипотенуза - она же большая диагональ, = 10 см. Остаётся по Пифагору найти второй катет (он же меньшая диагональ), х² = 10²-5²; х = √75 = 8.6602540378 (см).
Что и требовалось доказать!
Объяснение:Теорема: "Если при пересечении двух прямых секущей односторонние углы в сумме составляют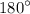 , то прямые параллельны".
, то прямые параллельны".
Что и требовалось доказать!
- - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Т.к.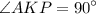 и
и 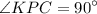
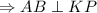 и
и 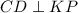 .
.
Признак: "Если две различные прямые на плоскости перпендикулярны к одной и той же прямой, то они параллельны".
Т.к. и
и 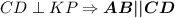 .
.
Что и требовалось доказать!
- - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1. Правильный пятиугольник, сторона = 1 см.
Отношение диагонали правильного пятиугольника к стороне = золотому сечению (то есть числу (1+√5)÷2).
Считаем: х÷1 = (1+√5)÷2
x = 1.6180339888 (см)
2.Правильный шестиугольник, сторона = 5 см.
При проведении меньшей диагонали получаем треугольник, у которого тупой угол = 120°, острые углы = по 30° каждый.
Решение 1. Меньшая диагональ правильного шестиугольника в √3 раз больше его стороны (это - свойство правильного шестиугольника), то есть = 5×√3 = 8.6602540378 (см).
Решение 2. Основано на правиле о том, что катет, лежащий против угла в 30°, равен половине гипотенузы. Нарисуй, и сразу все увидишь!
Если провести в правильном шестиугольнике и меньшую, и большую диагонали, то большая диагональ является гипотенузой прямоугольного треугольника, а меньшая диагональ является одним из катетов.
Получается, что нам именно и известен этот самый катет, лежащий напротив угла в 30°, он = 5 см. Тогда гипотенуза - она же большая диагональ, = 10 см. Остаётся по Пифагору найти второй катет (он же меньшая диагональ), х² = 10²-5²; х = √75 = 8.6602540378 (см).