1.
Катеты фиолетового треугольника: 16; 6
Гипотенуза равна:
Гипотенуза фиолетового треугольника равна: 17.1.
2.
Чтобы найти наибольший катет бледно-красного, вычтим те 4 сантиметра с нашей гипотенузы: 17.1-4 = 13.1
Теперь к этому числу добавим те 9 сантиметров (в правой нижней стороне красного треугольника): 13.1+9 = 22.1
Теперь нам известно 2 катета бледно-красного треугольника: 22.1; 7.
Гипотенуза её равна:
Вычтим с этого числа те 2 сантиметров(в правом верхнем углу бледно-красного треугольника): 23.18-2 = 21.18.
3.
Теперь нам известна гипотенуза жёлтого треугольника, и его катет.
Второй катет равен:
Теперь мы знаем 2 катета, и гипотенузу желтого треугольника.
4.
Прибавим к наибольшому катету 5 и 1(в правом и левом нижнем углу синего треугольника): 20.3+6 = 26.3.
Теперь нам известно 2 катета синего треугольника: 12; 26.3.
Гипотенуза равна: .
5.
Вычтим 11 сантиметров с гипотенузы синего треугольника (левый нижний угол зелёного треугольника): 28.9-11 = 17.9.
Теперь нам известно 2 катета зелёного треугольника: 14; 17.9.
6.
Нам известна гипотенуза, и один катет розового треугольника: 16; 22.72.
Второй катет равен: .
7. Прибавим к этому числу 5 сантиметров (нижний левый угол голубого треугольника): 16.13+5 = 21.13.
Теперь нам известно 2 катета: 5; 21.13
Найдём гипотенузу:
Вывод: самая верхняя гипотенуза равна 21,71 сантиметров.
Объяснение:
1)
Sкв=10²=10*10=100 см² площадь квадрата.
АС=АВ*√2=10√2 см диагональ квадрата и диаметр окружности.
R=1/2*AC=1/2*10√2=5√2 см.
Sкр=π*R²=(5√2)²*3,14=50*3,17=157 см² площадь круга.
Sз.ф.=Sкр-Sкв=157-100=57см²
ответ: 57 см²
2)
tg<CAD=CD/AD
tg30°=1/√3
1/√3=CD/6
CD=6/√3=2√3.
Sпр=СD*AD=2√3*6=12√3см² площадь прямоугольника.
cos<CAD=AD/AC
cos30°=√3/2
√3/2=6/AC
AC=6*2/√3=4√3
R=AC/2=4√3/2=2√3 см радиус окружности.
Sкр=π*R²=(2√3)²*3,14=12*3,14=37,68 см²
Sз.ф.=Sкр-Sпр=37,68-12√3 см²
ответ: площадь закрашенной фигуры 37,68-12√3 см²
Обозначения:
Sкр- площадь круга.
Sкв.- площадь квадрата
Sпр- площадь прямоугольника
Sз.ф.- площадь закрашенной фигуры.
Решено- zmeura1204
1.
Катеты фиолетового треугольника: 16; 6
Гипотенуза равна: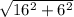
Гипотенуза фиолетового треугольника равна: 17.1.
2.
Чтобы найти наибольший катет бледно-красного, вычтим те 4 сантиметра с нашей гипотенузы: 17.1-4 = 13.1
Теперь к этому числу добавим те 9 сантиметров (в правой нижней стороне красного треугольника): 13.1+9 = 22.1
Теперь нам известно 2 катета бледно-красного треугольника: 22.1; 7.
Гипотенуза её равна:
Вычтим с этого числа те 2 сантиметров(в правом верхнем углу бледно-красного треугольника): 23.18-2 = 21.18.
3.
Теперь нам известна гипотенуза жёлтого треугольника, и его катет.
Второй катет равен: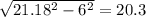
Теперь мы знаем 2 катета, и гипотенузу желтого треугольника.
4.
Прибавим к наибольшому катету 5 и 1(в правом и левом нижнем углу синего треугольника): 20.3+6 = 26.3.
Теперь нам известно 2 катета синего треугольника: 12; 26.3.
Гипотенуза равна: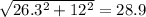 .
.
5.
Вычтим 11 сантиметров с гипотенузы синего треугольника (левый нижний угол зелёного треугольника): 28.9-11 = 17.9.
Теперь нам известно 2 катета зелёного треугольника: 14; 17.9.
Гипотенуза равна: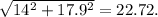
6.
Нам известна гипотенуза, и один катет розового треугольника: 16; 22.72.
Второй катет равен: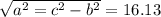 .
.
7. Прибавим к этому числу 5 сантиметров (нижний левый угол голубого треугольника): 16.13+5 = 21.13.
Теперь нам известно 2 катета: 5; 21.13
Найдём гипотенузу: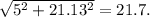
Вывод: самая верхняя гипотенуза равна 21,71 сантиметров.
Объяснение:
1)
Sкв=10²=10*10=100 см² площадь квадрата.
АС=АВ*√2=10√2 см диагональ квадрата и диаметр окружности.
R=1/2*AC=1/2*10√2=5√2 см.
Sкр=π*R²=(5√2)²*3,14=50*3,17=157 см² площадь круга.
Sз.ф.=Sкр-Sкв=157-100=57см²
ответ: 57 см²
2)
tg<CAD=CD/AD
tg30°=1/√3
1/√3=CD/6
CD=6/√3=2√3.
Sпр=СD*AD=2√3*6=12√3см² площадь прямоугольника.
cos<CAD=AD/AC
cos30°=√3/2
√3/2=6/AC
AC=6*2/√3=4√3
R=AC/2=4√3/2=2√3 см радиус окружности.
Sкр=π*R²=(2√3)²*3,14=12*3,14=37,68 см²
Sз.ф.=Sкр-Sпр=37,68-12√3 см²
ответ: площадь закрашенной фигуры 37,68-12√3 см²
Обозначения:
Sкр- площадь круга.
Sкв.- площадь квадрата
Sпр- площадь прямоугольника
Sз.ф.- площадь закрашенной фигуры.
Решено- zmeura1204