Нужна
точка к находится на расстоянии 4 см от каждой
13 вершин правильного треугольника авс. знайдить
длину стороны треугольника, если точка к отдалена от плоскости авс на 2 см.

Показать ответ

Ответ:

Vika2947

19.09.2020 13:13

найдем ДС по теореме пифагора, так как ДА перпендикулярна плоскости основания, значит она и перпендикулярно любой линии лежащей в данной плоскости. ДС = sqrt (20*20+21*21) = 29. Чтобы найти площадь боковой поверхности надо сложить площади треугольников АДС, АДВ, СДВ, найдем их. Площадь АДС = 1/2*20*21 = 210.

Площадь АДВ = 1/2*20*29=290. найдем сторону СВ по теореме пифагора = sqrt (29*29 - 21*21) = 20. Рассмотрев треугольник СДВ замечаем что все его стороны равны сторонам треугольника АДВ => и площади у них будут одинаковы. ответ S(бок поверхн) = 290*2+210 = 790

0,0(0 оценок)

Ответ:

chinenko88

21.06.2022 20:56

описаная окружность, тогда образуется три равные дуги с центр углом 120 град,

тогда площадь треуг = 3*1/2*R*R*sin 120=

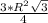
= $\frac{3*R^2\sqrt{3}}{4}$

Квадрат состоит из 4 равных треугольников, причем радиусы - половины диагоналей образуют угол 90 град, тогда

Sквадрата =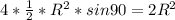 $4*\frac{1}{2}*R^2*sin90=2R^2$

Sквадр - Sтреуг=18,5, подставим, получим :

$2R^2 - \frac{3*R^2*\sqrt{3}}{4}=18.5\\ \\8R^2-3*R^2*\sqrt{3}=74\\ \\R^2*(8-3*\sqrt{3})=74\\ \\R^2=\frac{74}{(8-3*\sqrt{3})}$

В описанной окружности правильного шестиугольника получается 6 равносторонних треугольника со стороной = R, тогда

Sшестиуг =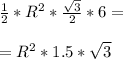 $\frac{1}{2}*R^2*\frac{\sqrt{3}}{2}*6=\\ \\=R^2*1.5*\sqrt{3}$

Подставим значение R^2, получим :

Sшестиуг=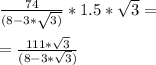 $\frac{74}{(8-3*\sqrt{3)}}*1.5*\sqrt{3}=\\ \\=\frac{111*\sqrt{3}}{(8-3*\sqrt{3})}$

ответ: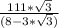 $\frac{111*\sqrt{3}}{(8-3*\sqrt{3})}$

Домножив числитель и знаменатель на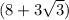 $(8+3\sqrt{3})$

получим:

$\frac{111*\sqrt{3}}{(8-3*\sqrt{3})}*\frac{(8+3\sqrt{3})}{(8+3\sqrt{3})}=\frac{888\sqrt{3}+999}{(8-3*\sqrt{3})*(8+3\sqrt{3})}=\\ \\=\frac{111*(8\sqrt{3}+9)}{64-24\sqrt{3}+24\sqrt{3}-27}=\\ \\=\frac{111*(8\sqrt{3}+9)}{37}=3(8\sqrt{3}+9)$