А1 т.к АB = 24, а AC =25 , То S=ab S= AB*AC=25*24°600см^2 A2 ТК как в прямоугольном треугольник BAC угол A=90 градусов , а угол С=60 градусов , то угол В равен угол А-угол В В=90-60=30градусов катет лежащий против угла 30 градусов равен половине гипотенузы , следовательно AC= 1/2BC AC=2:40=20 по теореме Пифагора находим второй катет bc^2= ab^2+ac^2 ab^2=bc^2-ac^2 ab^2=1600 -400=1200 ab=√1200=20√3 S=1/2ab=1/2 20√3*20=200√3( не уверен) (извини только два смогу пока-что , напиши в комментах через 2 часа ) я потом решу
Получаем 2 прямоугольных треугольника с катетами: х и 5 у первого и 15-х и 5 у второго.
Площадь прямоугольного треугольника равна половине произведения его катетов, т.е. имеем 5х/2 - площадь первого и 5*(15-х)/2 - площадь второго. Сумма площадей этих прямоугольных треугольников искомой равна площади исходного треугольника:
S=
S=
S=37.5
2.
Обозначим неизвестный катет за x. Тогда x===9
S=
S=12*9/2=54 см²
3.
Площадь ромба равна сумме площадей прямоугольных треугольников, которые он образовывает своими диагоналями. Соответственно, если имеем диагонали 20 и 40, то S одного треугольника=10*20/2=100 см²
S ромба равна 4*100=400 см²
Периметр ромба будет равен сумме 4-х гипотенуз, вышеупомянутых треугольников, а так как они равны, то
т.к АB = 24, а AC =25 , То S=ab
S= AB*AC=25*24°600см^2
A2
ТК как в прямоугольном треугольник BAC угол A=90 градусов , а угол С=60 градусов , то угол В равен угол А-угол В
В=90-60=30градусов
катет лежащий против угла 30 градусов равен половине гипотенузы , следовательно
AC= 1/2BC
AC=2:40=20
по теореме Пифагора находим второй катет
bc^2= ab^2+ac^2
ab^2=bc^2-ac^2
ab^2=1600 -400=1200
ab=√1200=20√3
S=1/2ab=1/2 20√3*20=200√3( не уверен)
(извини только два смогу пока-что , напиши в комментах через 2 часа ) я потом решу
1.
Получаем 2 прямоугольных треугольника с катетами: х и 5 у первого и 15-х и 5 у второго.
Площадь прямоугольного треугольника равна половине произведения его катетов, т.е. имеем 5х/2 - площадь первого и 5*(15-х)/2 - площадь второго. Сумма площадей этих прямоугольных треугольников искомой равна площади исходного треугольника:
S=
S=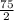
S=37.5
2.
Обозначим неизвестный катет за x. Тогда x= =
= =9
=9
S=
S=12*9/2=54 см²
3.
Площадь ромба равна сумме площадей прямоугольных треугольников, которые он образовывает своими диагоналями. Соответственно, если имеем диагонали 20 и 40, то S одного треугольника=10*20/2=100 см²
S ромба равна 4*100=400 см²
Периметр ромба будет равен сумме 4-х гипотенуз, вышеупомянутых треугольников, а так как они равны, то
P=4*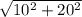 =4*
=4* ≈4*22.36≈89.44 см²
≈4*22.36≈89.44 см²