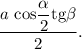Нужна основанием четырёхугольной пирамиды является ромб с острым углом α и меньшей диагональю а. все двугранные углы при основании пирамиды равны β. найдите: 1) площадь полной поверхности пирамиды; 2) высоту пирамиды.
Пусть — четырёхугольная пирамида, в основании которой ромб Меньшая диагональ ромба и острый угол высота пирамиды, значит, , следовательно так как — проекция на плоскость ⇒ по теореме о трёх перпендикуляров (ТТП) , следовательно, — линейный угол двугранного угла при ребре так как все двугранные углы при основании равны, то точка О — центр вписанной окружности, то есть
Найти:
Решение. Ромб состоит из четырёх равных прямоугольных треугольников:
Рассмотрим
Значит, диагональ
Рассмотрим
Высота ромба
Площадь основания пирамиды
Рассмотрим
Определим площадь треугольника
Из-за того, что у ромба все стороны равны и все двугранные углы при основании равны, то все боковые грани пирамиды будут тоже равны. Следовательно, площадь боковой поверхности
Теперь, зная площадь основания и боковой поверхности пирамиды можно найти площадь полной поверхности:
ответ: площадь полной поверхности пирамиды равна высота пирамиды равна
Пусть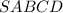 — четырёхугольная пирамида, в основании которой ромб
— четырёхугольная пирамида, в основании которой ромб 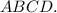 Меньшая диагональ ромба
Меньшая диагональ ромба 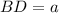 и острый угол
и острый угол 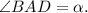
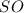 высота пирамиды, значит,
высота пирамиды, значит, 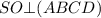 , следовательно
, следовательно 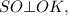 так как
так как 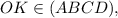
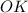 — проекция
— проекция 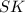 на плоскость
на плоскость 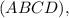
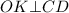 ⇒ по теореме о трёх перпендикуляров (ТТП)
⇒ по теореме о трёх перпендикуляров (ТТП) 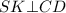 , следовательно,
, следовательно, 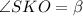 — линейный угол двугранного угла при ребре
— линейный угол двугранного угла при ребре 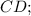 так как все двугранные углы при основании равны, то точка О — центр вписанной окружности, то есть
так как все двугранные углы при основании равны, то точка О — центр вписанной окружности, то есть 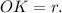
Найти: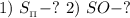
Решение. Ромб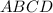 состоит из четырёх равных прямоугольных треугольников:
состоит из четырёх равных прямоугольных треугольников: 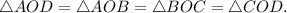
Рассмотрим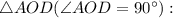
Значит, диагональ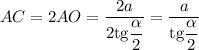
Рассмотрим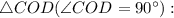
Высота ромба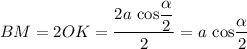
Площадь основания пирамиды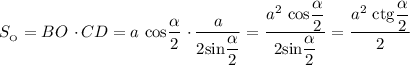
Рассмотрим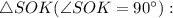
Определим площадь треугольника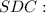
Из-за того, что у ромба все стороны равны и все двугранные углы при основании равны, то все боковые грани пирамиды будут тоже равны. Следовательно, площадь боковой поверхности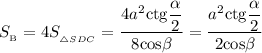
Теперь, зная площадь основания и боковой поверхности пирамиды можно найти площадь полной поверхности:
ответ: площадь полной поверхности пирамиды равна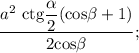 высота пирамиды равна
высота пирамиды равна