Нужен совет, правильно ли решил ,
условие :
изобразить область на комплексной плоскости, заданную неравенсвами
1" class="latex-formula" id="TexFormula1" src="https://tex.z-dn.net/?f=%20%7Cz%20%2B%20i%7C%20%3E%201" title=" |z + i| > 1">

​

Медиана, проведённая к большему катету, равна 5√13 ≈ 18,03; гипотенуза делится точкой касания с вписанной окружностью на отрезки длиной 15 и 10.

(см. рисунок - в прикреплении)

Объяснение:

1) Медиана АМ, проведённая к большему катету ВС, делит его на 2 равных отрезка СМ = МВ = 10, и, таким образом, является гипотенузой в прямоугольном треугольнике МСА с катетами МС = 10 и АС = 15. Согласно теореме Пифагора, гипотенуза АМ равна корню квадратному из суммы квадратов катетов:

АМ = √(МС² + АС²) = √(10² + 15²) = √(100 + 225) = √325 = √(25 · 13) = 5√13 ≈ 5 · 3,6056 ≈ 18,03

2) Радиус r окружности, вписанной в прямоугольный треугольник, рассчитывается по формуле:

r = (a + b - c) : 2,

где а и b - катеты прямоугольного треугольника, с - его гипотенуза.

Гипотенуза АВ прямоугольного Δ АВС равна:

АВ = √(АС² + ВС²) = √(15²+20²) = √(225 + 400) = √625 = 25

Таким образом, радиус окружности, вписанной в Δ АВС, равен:

r = (АС + ВС - АВ) : 2 = (15 + 20 - 25) : 2 = (35 - 25) : 2 = 10 : 2 = 5

3) Вписанная окружность касается катета АС в точке D, а гипотенузы АВ в точке Е. Так как CD = r = 5, то АD = АС - СD = 15 - 5 = 10.

Отрезки касательных, проведённых к окружности из одной точки, равны.

Следовательно, AD = AE = 10

4) ВЕ = АВ - АЕ = 25 - 10 = 15

Таким образом, гипотенуза АВ делится точкой касания Е с вписанной окружностью на отрезки ВЕ длиной 15 и АЕ длиной 10.

ответ: медиана, проведённая к большему катету, равна 5√13 ≈ 18,03; гипотенуза делится точкой касания с вписанной окружностью на отрезки длиной 15 и 10.

24 м² и 30°.

Объяснение:

Дано:

АВСА1В1С1-правильная усеченная пирамида

АВ=ВС=АС=8 см

А1В1=В1С1=А1С1=5 см

OO1= 3 см

Найти: площадь сечения и угол между ним и нижним основанием

1) СА1В - искомое сечение, т.к. точки А1С и А1В находятся в одних плоскостях.

2)Ось правильной усеченной пирамиды совпадает с осью соответствующей полной пирамиды, поэтому OO1 является высотой усеченной пирамиды.  О1  — центр окружности, описанной около треугольника  А1В1С1, О - центр окружности, вписанной в треугольник  АВС.

Формула для радиуса описанной окружности около равностороннего треугольника:

R=а*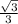

Формула для радиуса вписанной окружности в равносторонний треугольник:

r= а*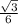

R=А1О1=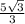

r=ОН==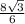

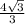
Проведем АН⊥ВС в ΔАВС.  ОО1⊥(АВС)⇒ОО1⊥АН.  

По теореме о трех перпендикулярах А1Н⊥ВС в ΔСА1В.

Угол ∠А1НА - линейный угол искомого двугранного угла.

Рассмотрим ΔА1О1К и ΔНОК.

∠А1О1К=∠НОК=90°, ∠А1КО1=∠НКО как вертикальные.

⇒ ΔА1О1К подобен ΔНОК ( по двум углам).

Из подобия Δ следует:

А1О1:ОН=О1К:КО

А1О1*КО=ОН*О1К

Пусть О1К= х, тогда КО=(3-х):

* (3-х) =

5√3(3-х)=4√3*х

9√3х=15√3

х=5/3

О1К = 5/3,

КО=3-5/3=4/3

ΔА1О1К(∠О1=90°): по т.Пифагора

А1К=√(А1О1²+О1К²)= √(75/9+25/9)=√(100/9)=10/3

ΔОКН(∠О=90°): по т.Пифагора

КН=√(ОН²+КО²)=√(16/9+48/9)=8/3

А1Н=А1К+КН=10/3+8/3=18/3=6 см

Площадь искомого сечения это площадь ΔСА1В:

S = 1/2 * ВС* А1Н = 1/2 * 8 * 6 = 24 см²

3) Рассмотрим ΔКОН(∠О=90°)

tg ∠KHO = KO/OH = : =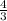

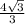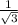
Тогда ∠KHO = 30°.

Т.к. ∠А1НА = ∠KHO, то ∠А1НА=30°