можно посчитать длину СС1 исходя из соотношения проекций АА1 и ВВ1. Сложив 8 и 3, получим 11, соответственно общая длина АВ в проекции будет равна 11. Разделив 11 на 5 отрезков (т. к. отношение АС и СВ 2:3) получим, что длина проекции условного отрезка равна 2,2. Умножив это значение на 3, получаем 6,6. Это была бы длина отрезка СС1, если бы точкой пересечения плоскости а была бы точка В, но постольку поскольку точка В лежит на противоположной стороне отрезка нужно вычесть длину отрезка ВВ1 из 6,6. Получается, что длина отрезка СС1=6,6-3=3,6
1) неизвестный отрезок является гипотенузой прямоугольного треугольника:
2) неизвестный отрезок является высотой, проведённой к основанию, в равнобедренном треугольнике. Как известно, высота, проведённая к основанию, в равнобедренном треугольнике является также медианой и биссектрисой. Следовательно неизвестный отрезок делит основание пополам и является катетом в прямоугольном треугольнике с гипотенузой равной 5 и катетом равным :
3) Здесь имеется три неизвестных отрезка, два из которых равны.
Начнём с высоты, опять же она проведена к основанию в равнобедренном треугольнике, а значит является и медианой и биссектрисой. А медиана проведённая к гипотенузе в прямоугольном треугольнике равна половине гипотенузы:
Нам известно, что оставшиеся неизвестные отрезки являются катетами в прямоугольном треугольнике и что они равны. Нам известна гипотенуза этого треугольника:
ответ:СС1=6,6-3=3,6
Объяснение:
можно посчитать длину СС1 исходя из соотношения проекций АА1 и ВВ1. Сложив 8 и 3, получим 11, соответственно общая длина АВ в проекции будет равна 11. Разделив 11 на 5 отрезков (т. к. отношение АС и СВ 2:3) получим, что длина проекции условного отрезка равна 2,2. Умножив это значение на 3, получаем 6,6. Это была бы длина отрезка СС1, если бы точкой пересечения плоскости а была бы точка В, но постольку поскольку точка В лежит на противоположной стороне отрезка нужно вычесть длину отрезка ВВ1 из 6,6. Получается, что длина отрезка СС1=6,6-3=3,6
Объяснение:
Обозначим неизвестные отрезки за x
1) неизвестный отрезок является гипотенузой прямоугольного треугольника:
2) неизвестный отрезок является высотой, проведённой к основанию, в равнобедренном треугольнике. Как известно, высота, проведённая к основанию, в равнобедренном треугольнике является также медианой и биссектрисой. Следовательно неизвестный отрезок делит основание пополам и является катетом в прямоугольном треугольнике с гипотенузой равной 5 и катетом равным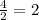 :
:
3) Здесь имеется три неизвестных отрезка, два из которых равны.
Начнём с высоты, опять же она проведена к основанию в равнобедренном треугольнике, а значит является и медианой и биссектрисой. А медиана проведённая к гипотенузе в прямоугольном треугольнике равна половине гипотенузы:
Нам известно, что оставшиеся неизвестные отрезки являются катетами в прямоугольном треугольнике и что они равны. Нам известна гипотенуза этого треугольника: