Как показано на рисунке 611 — AF == AD = AD/2; BC == AF == FD = AD/2.
Теорема такова: если отрезок, проведённый из двух сторон — равен половине третьей стороны, то этот отрезок — средняя линия.
Как мы видим, на стороне AM, центр — B, на стороне AD, центр — F, а на стороне MD, центр — C. Тоесть отезок FC — проведён с центров двух сторон, тоесть — она средняя линия.
Отметим ещё то, что средняя линия параллельна своей противоположной стороне(факт), тоесть: BC║AD.
FC — также средняя линия, тоесть — она равна половине своей противоположной стороны, тоесть: AM = 10 ⇒ CF = 10/2 = 5.
Вывод: CF = 5.
1.
Теорема о 30-градусном угле такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: BC = AB/2 ⇒ BC = 4.
Для вычисления площади прямоугольного треугольника — нам надо знать 2 катета(гипотенуза к чёрту не нужна).
А чтобы найти катет AC — зная первый катет, и гипотенузу — используем простейшую теорему Пифагора:
Формула вычисления площади прямоугольного треугольника:
Внимание! Эта формула работает только с прямоугольным треугольником, так как прямоугольный треугольник имеет один прямой угол.
Вычисление площади обычного произвольного треугольника — содержит альтернативную формулу!
2.
Так как один из острых углов равен 45°, то второй острый угол равен: 90-45 = 45° ⇒ <M == <N = 45° ⇒ KM == KN = 4.
Зная 2 катета — найдём гипотенузу NM:
Вывод: NM = 5.66.
3.
Формула вычисления боковой стороны, зная угол, противолежащий основанию, и основание: .
4.
Формула вычисления биссектрисы, проведённую через острый угол в прямоугольном треугольнике такова:
5.
Формула вычисления диагонали CD — зная 2 стороны:
Формула вычисления любой стороны прямоугольника, зная диагональ:
В рассказе М.А.Осоргина “Пенсне” вещи “живут своей особенной жизнью”. Особенно интересна для меня жизнь Карандаша, который имел “страсть к путешествиям”. Он постоянно прятался и пропадал. Вот Карандаш исчез в очередной раз. Обыскали весь дом, но найти пропажу не удалось.
Входная дверь была приоткрыта, а графитовый след на полу говорил, что предмет сбежал из дома. Начали думать и гадать, куда мог отправиться Карандаш. Предполагали разное, но никто не знал точно, что же произошло.
два дня. И утром под кроватью беглеца обнаружили. Он был пыльный и поцарапанный, на кончике виднелись следы зубов. Стало ясно, что Карандашу захотелось посмотреть, что находится за пределами квартиры, и он ушел гулять, не подозревая, какие опасности ждали его на улице. Сначала он упал в лужу , промок и долго-долго лежал под палящим солнцем,пока не высох. Затем из-за угла выскочила огромная рыжая собака и напала на него. Она больно укусила Карандаша, да ещё и поцарапала. Бедный Карандаш еле вырвался из её цепких лап. Он так перепугался, что не мог двигаться, поэтому лежал без чувств на пыльной дороге и не смел пошевелиться, потом встал и побрёл куда-то. Вдруг перед ним возник родной дом, Карандаш радостно вздохнул, весело подпрыгнул, тихо пробрался в открытое окно и упал под кровать.
10.
Как показано на рисунке 611 — AF == AD = AD/2; BC == AF == FD = AD/2.
Теорема такова: если отрезок, проведённый из двух сторон — равен половине третьей стороны, то этот отрезок — средняя линия.
Как мы видим, на стороне AM, центр — B, на стороне AD, центр — F, а на стороне MD, центр — C. Тоесть отезок FC — проведён с центров двух сторон, тоесть — она средняя линия.
Отметим ещё то, что средняя линия параллельна своей противоположной стороне(факт), тоесть: BC║AD.
FC — также средняя линия, тоесть — она равна половине своей противоположной стороны, тоесть: AM = 10 ⇒ CF = 10/2 = 5.
Вывод: CF = 5.
1.
Теорема о 30-градусном угле такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: BC = AB/2 ⇒ BC = 4.
Для вычисления площади прямоугольного треугольника — нам надо знать 2 катета(гипотенуза к чёрту не нужна).
А чтобы найти катет AC — зная первый катет, и гипотенузу — используем простейшую теорему Пифагора:
Формула вычисления площади прямоугольного треугольника: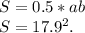
Внимание! Эта формула работает только с прямоугольным треугольником, так как прямоугольный треугольник имеет один прямой угол.
Вычисление площади обычного произвольного треугольника — содержит альтернативную формулу!
2.
Так как один из острых углов равен 45°, то второй острый угол равен: 90-45 = 45° ⇒ <M == <N = 45° ⇒ KM == KN = 4.
Зная 2 катета — найдём гипотенузу NM:
Вывод: NM = 5.66.
3.
Формула вычисления боковой стороны, зная угол, противолежащий основанию, и основание: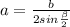 .
.
4.
Формула вычисления биссектрисы, проведённую через острый угол в прямоугольном треугольнике такова:
5.
Формула вычисления диагонали CD — зная 2 стороны: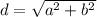
Формула вычисления любой стороны прямоугольника, зная диагональ: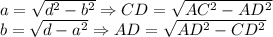
Формула вычисления площади прямоугольника: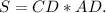
В рассказе М.А.Осоргина “Пенсне” вещи “живут своей особенной жизнью”. Особенно интересна для меня жизнь Карандаша, который имел “страсть к путешествиям”. Он постоянно прятался и пропадал. Вот Карандаш исчез в очередной раз. Обыскали весь дом, но найти пропажу не удалось.
Входная дверь была приоткрыта, а графитовый след на полу говорил, что предмет сбежал из дома. Начали думать и гадать, куда мог отправиться Карандаш. Предполагали разное, но никто не знал точно, что же произошло.
два дня. И утром под кроватью беглеца обнаружили. Он был пыльный и поцарапанный, на кончике виднелись следы зубов. Стало ясно, что Карандашу захотелось посмотреть, что находится за пределами квартиры, и он ушел гулять, не подозревая, какие опасности ждали его на улице. Сначала он упал в лужу , промок и долго-долго лежал под палящим солнцем,пока не высох. Затем из-за угла выскочила огромная рыжая собака и напала на него. Она больно укусила Карандаша, да ещё и поцарапала. Бедный Карандаш еле вырвался из её цепких лап. Он так перепугался, что не мог двигаться, поэтому лежал без чувств на пыльной дороге и не смел пошевелиться, потом встал и побрёл куда-то. Вдруг перед ним возник родной дом, Карандаш радостно вздохнул, весело подпрыгнул, тихо пробрался в открытое окно и упал под кровать.
Вот так закончились приключения Карандаша.
Объяснение: