Найдите углы параллелограмма если сумма двух из них равна
а) 80 градусов б) 100 градусов в)160 градусов

Показать ответ

Ответ:

Алинаwlis

15.03.2020 10:55

Нам дан ΔABC, AB=BC=25 см. AK,BH,CL - медианы треугольника.

AC=14 см.

AK,BH,CL - ?

Медиана , проведенная к основанию АС является высотой ( по свойству равнобедренного треугольника ). AH=HC = 7 см. Отсюда из ΔBHA(∠BHA=90°) за Т.Пифагора найдем BH:

$BH=\sqrt{BA^2-AH^2}\\\\BH=\sqrt{25^2-7^2}\\\\BH=\sqrt{625-49}\\\\BH=\sqrt{574}=24$ .

BH = 24 см. Медианы треугольника пересекаются в точке, и делятся в соотношении 2 : 1 считая от вершины.

Пусть OH=x , тогда BH = 2x.

BH=BO+OH

24=2x+x

24=3x

x=8 см.

Отсюда OH = 8 см.

Из ΔOHA(∠OHA=90°) за Т.Пифагора найдем AO.

$AO=\sqrt{AH^2+OH^2}\\\\AO=\sqrt{8^2+7^2}\\\\AO=\sqrt{64+49}=\sqrt{113}$ .

Пусть OK= x, тогда AO=2x ( из свойства медиан, которые пересекаются в одной точке ) , тогда имеем уравнения:

$2x=\sqrt{113}\\\\x=\frac{\sqrt{113} }{2}$

AK = AO + OK

$AK=\sqrt{113}+\frac{\sqrt{113} }{2}=\frac{3\sqrt{113} }{2}$ см.

AK=CL ( по свойству равнобедренного треугольника )

ответ: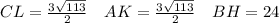 $CL=\frac{3\sqrt{113} }{2}\ \ \ AK=\frac{3\sqrt{113} }{2}\ \ \ BH=24$ сантиметров.

Найти медианы треугольника со сторонами 25,25,14

0,0(0 оценок)

Ответ:

jdkxnVAkx

15.03.2020 10:55

Пусть в ∆ АВС стороны АС=14, АВ=ВС=25. ВН и АМ - медианы. О - точка пересечения медиан.

АН=СН=14:2=7. Т.к. ∆ АВС - равнобедренный, медиана ВН является и высотой. По т.Пифагора ВН=√(АВ²-АН²)= √(25²-7²)=24. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины. ВО=2НО, => ВН=3ОН и ОН=ВН:3=24:3=8 Из прямоугольного ∆ АОН по т.Пифагора ОН=√(АН²+ОН²)=√(7²+8²)=√113. Тогда ОМ=0,5•√113, а медиана АМ=3ОМ=1,5√13. Треугольник АВС - равнобедренный, поэтому медиана из С равна АМ=1,5√113