1. 53°
2. 45°, 45°
3. А=45°, С=45°, DBC=45°
4. 50°
9. 144°
10. 132°
11. 140°
12. 45°
Объяснение:
1: B = 180°- (C+A) = 180°- (90°+37°)=53°
2 т.к. треугольник равнобедренный, углы у основания равны.
Это значит: 2x+90=180°. x=45°
3. B = 90°, треугольник равнобедренный. Значит углы у основания равны - 2x+90=180°. x=45° (A и C).
DBC=45° т.к. BD - биссектриса.
Треугольник BDC равнобедренный т.к. углы у основвния равны.
4. C (в треугольнике DBC и ADC) = 180°-(D+B) = 180°-90°-70° = 20°
Угол ADC смежный = 180°-70° = 110°
А = 180°-(D+C) = 180°-(20°+110°)=50°
9. т.к. односторонние углы у параллельных прямых дают в сумме 180°, x(1-й угол), 4х(2-й угол)
= x+4x=180°, x= 36°(1-й угол). 4х = 144°(2-й угол).
Т.к. угол 2 и угол 3 - вертикальные, угол 3= углу 2= 144°
10. Т.к. х || у, соответственные углы равны - угол 1 = углу 2 = 96÷2= 48°
Угол 3 = 180°-угол 1 (т.к. углы смежные) = 180°-48°=132°
11. Угол 3 = углу 2(т.к. вертикальные углы).
Т.к. z || q сумма односторонних углов = 180° - т.е. угол 3 и угол 1 (1 угол как бы не односторонний, но вертикальный для одностороннего, которого нет на рисунке)
Угол 1 = 2х, а 3 угол = 7х. 7х+2х=180° = 9х = 180°. 1х=20°.
Т.к. угол 3 = 7х = 20°×7=140°.
12.Т.к. t || m сумма односторонних углов = 180°
Т.е. угол 2+угол 1 = 180°
Т.к. угол 2 на 90° > угла 1 (х= 1 угол, х+90° = 2 угол)
Т.е х+(х+90°)=180°. х= 45°
Угол 1 и угол 3 - вертикальные. Т.е угол 1 = углу 3. Т.е угол 3 = 45°
ответ: КК1 = 12 см
Объяснение: Исправим условие
Отрезок MN не пересекает плоскость а. Точка К принадлежит
отрезку MN. Через точки M, и N проведены параллельные
прямые, пересекающие плоскость а в точках М1, K1, и N 1
соответственно. Найдите длину отрезка КК1, если MM1 = 6 см,
NN1 = 21 см и МК: KN = 2:3.
Теперь решим.
Для начала проведем параллельно плоскости прямую МН. тогда Поучится треугольник MNH сторона NH которого 6 см,
а МК:КN = 2:3. Треугольники МКЕ и МNH подобные, так как угол М общий, а углы МКЕ и MNH равны как соответственные.
Тогда MN = 5х, а МК = 2х
МН:КЕ = 5х:2х=5:2, значит КЕ = МН = = 6 с м
Итак, отрезок КЕ = 6 см
КК1 = КЕ+ЕК1 = 6+6=12 см
КК1 = 12 см
1. 53°
2. 45°, 45°
3. А=45°, С=45°, DBC=45°
4. 50°
9. 144°
10. 132°
11. 140°
12. 45°
Объяснение:
1: B = 180°- (C+A) = 180°- (90°+37°)=53°
2 т.к. треугольник равнобедренный, углы у основания равны.
Это значит: 2x+90=180°. x=45°
3. B = 90°, треугольник равнобедренный. Значит углы у основания равны - 2x+90=180°. x=45° (A и C).
DBC=45° т.к. BD - биссектриса.
Треугольник BDC равнобедренный т.к. углы у основвния равны.
4. C (в треугольнике DBC и ADC) = 180°-(D+B) = 180°-90°-70° = 20°
Угол ADC смежный = 180°-70° = 110°
А = 180°-(D+C) = 180°-(20°+110°)=50°
9. т.к. односторонние углы у параллельных прямых дают в сумме 180°, x(1-й угол), 4х(2-й угол)
= x+4x=180°, x= 36°(1-й угол). 4х = 144°(2-й угол).
Т.к. угол 2 и угол 3 - вертикальные, угол 3= углу 2= 144°
10. Т.к. х || у, соответственные углы равны - угол 1 = углу 2 = 96÷2= 48°
Угол 3 = 180°-угол 1 (т.к. углы смежные) = 180°-48°=132°
11. Угол 3 = углу 2(т.к. вертикальные углы).
Т.к. z || q сумма односторонних углов = 180° - т.е. угол 3 и угол 1 (1 угол как бы не односторонний, но вертикальный для одностороннего, которого нет на рисунке)
Угол 1 = 2х, а 3 угол = 7х. 7х+2х=180° = 9х = 180°. 1х=20°.
Т.к. угол 3 = 7х = 20°×7=140°.
12.Т.к. t || m сумма односторонних углов = 180°
Т.е. угол 2+угол 1 = 180°
Т.к. угол 2 на 90° > угла 1 (х= 1 угол, х+90° = 2 угол)
Т.е х+(х+90°)=180°. х= 45°
Угол 1 и угол 3 - вертикальные. Т.е угол 1 = углу 3. Т.е угол 3 = 45°
ответ: КК1 = 12 см
Объяснение: Исправим условие
Отрезок MN не пересекает плоскость а. Точка К принадлежит
отрезку MN. Через точки M, и N проведены параллельные
прямые, пересекающие плоскость а в точках М1, K1, и N 1
соответственно. Найдите длину отрезка КК1, если MM1 = 6 см,
NN1 = 21 см и МК: KN = 2:3.
Теперь решим.
Для начала проведем параллельно плоскости прямую МН. тогда Поучится треугольник MNH сторона NH которого 6 см,
а МК:КN = 2:3. Треугольники МКЕ и МNH подобные, так как угол М общий, а углы МКЕ и MNH равны как соответственные.
Тогда MN = 5х, а МК = 2х
МН:КЕ = 5х:2х=5:2, значит КЕ =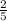 МН =
МН = 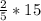 = 6 с м
= 6 с м
Итак, отрезок КЕ = 6 см
КК1 = КЕ+ЕК1 = 6+6=12 см
КК1 = 12 см