Найдите площадь ортогональной проекции квадрата с диагональю 4 см, если угол между плоскостью квадрата и его проекцией равен: ; б) 45°.

Показать ответ

Ответ:

Зоромдед

20.08.2021 06:35

Дано:
- треугольник АВС, биссектриса ВД, вписанная окружность с центром О,
- АВ = х,
- ВС = х + 1,
- АС = 15,
- ВО:ОД = 9:5.

Деление биссектрис точкой их пересечения (а это центр вписанной окружности) определяется формулой:
ВО:ОД = (АВ + ВС)/АС = (х + х + 1) /15 = 9/5.
Сократим знаменатели на 5 и приведём к общему знаменателю:
2х + 1 = 3*9,
2х = 27 - 1 = 26,
х = 26/2 = 13 это сторона АВ.
Находим сторону ВС = 13 + 1 = 14.
Полупериметр р = (13+14+15)/2 = 21.
Площадь S треугольника АВС находим по формуле Герона:
S = √(p(p-a)(p-b)(p-c)) = √ 7056 = 84.
Тогда радиус вписанной окружности r = S/p = 84/21 = 4.

0,0(0 оценок)

Ответ:

YourTeaa

06.11.2021 03:48

ответ:

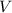призмы = 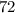см³.

Объяснение:

Обозначим данную призму буквами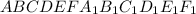 ABCD E F A_1B_1C_1D_1 E_1F_1 .

AD_1 = 8 см.

$\angle AD_1D = 30^{\circ}.$

============================================================

Если призма правильная, то она всегда будет прямой.

$\Rightarrow \triangle AD_1D$ - прямоугольный, где D_1D - высота данной призмы.

Рассмотрим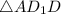 $\triangle AD_1D$ :

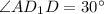$\angle AD_1D = 30^{\circ}$ , по условию.

Если угол прямоугольного треугольника равен $30^{\circ}$ , то напротив лежащий катет равен половине гипотенузы.

$\Rightarrow AD = \dfrac{AD_1}{2} = \dfrac{8}{2} = 4$ см.

По теореме Пифагора найдём высоту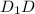 D_1D :

$D_1D^{2} = AD_1^{2} - AD^{2} = 8^{2} - 4^{2} = 48$

$D_1D = \sqrt{48} = 4\sqrt{3}$ см.

Рассмотрим нижнее основание данной призмы:

шестиугольник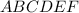 ABCD E F - правильный, так как данная призма тоже правильная.

- большая диагональ шестиугольника ABCD E F .

По свойству правильного шестиугольника,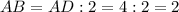 AB = AD : 2 = 4 : 2 = 2 см.

шестиугольника = $6 \cdot \dfrac{1}{2} \cdot AB \cdot AB \cdot sin(\dfrac{360^{\circ}}{6} )= 6 \cdot \dfrac{1}{2} \cdot 2 \cdot 2 \cdot sin(\dfrac{360^{\circ}}{6} )= 12 \cdot sin(60^{\circ}) = 6\sqrt{3}$ cм².