Найбільшу площу займають степові ландшафти​

Ч.т.д.

Объяснение:

Расстояние от точки до прямой - это длина перпендикуляра, проведённого из данной точки к этой прямой.

Так как пирамида правильная, значит её боковые грани представляют собой равнобедренные треугольники.

А это значит, что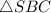 - равнобедренный.

И по свойству равнобедренного треугольника,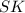 - медиана, биссектриса, высота .

, то есть - расстояние от точки S до BC.

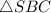По условию,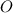 - середина .

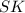Значит .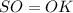

Также по условию,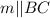 и m ∈ (SBC) .

- расстояние от S до m, а - расстояние от m до BC.

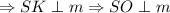Значит, расстояние от точки S до прямой m равно расстоянию между прямыми m и BC.

  Рассмотрим треугольник АВЕ. Он прямоугольный, ∠А равен 45°, следовательно, ∠В тоже равен 45°. Если у треуольника есть два равных угла, значит, треугольник равнобедренный, где АЕ=BE=5 см
  Рассмотрим треугольник CDF. Треугольник ABE и CDF равны (первый признак равенства треугольников), значит, сторона АЕ=FD=5 см.
  Рассмотрим прямоугольник BCEF. Т.к. две параллельные стороны прямоугольника равны, значит, EF=BC=3 см
  Теперь "соединяем" известные нам части стороны AD.
AD = AE + EF + FD = 5 + 3 + 5 = 13 см

ОТВЕТ: 13 см