L = (т.к. треугольник, образованный радиусом, высотой и образующей - прямоугольный) =
Sб.п.к.= П * 2 * = 2П
Sосн. = П * = 4П
Sп.п.к. = 2+4 = 6
Если нужна целая часть без П, то ответ будет 6, скорее всего
№2
Так как высота перпендикулярна основанию конуса, то высота, радиус и образующая составляют прямоугольный треугольник. Угол равный 30° лежит против катета, равного 10 см. По свойству угла в 30° (угол 30° лежит против катеты, равного половине гипотенузы), гипотенуза = 2*10 = 20 - образующая
1) 6
2) 17,32
3) 24
Объяснение:
№1
Pi буду писать как П
Sп.п.к. = Sб.п.к. + Sосн.
Sб.п.к. = П * R * L
Sосн. = П *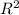
L =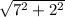 (т.к. треугольник, образованный радиусом, высотой и образующей - прямоугольный) =
(т.к. треугольник, образованный радиусом, высотой и образующей - прямоугольный) = 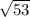
Sб.п.к.= П * 2 *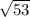 = 2
= 2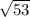 П
П
Sосн. = П *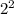 = 4П
= 4П
Sп.п.к. = 2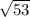 +4 = 6
+4 = 6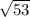
Если нужна целая часть без П, то ответ будет 6, скорее всего
№2
Так как высота перпендикулярна основанию конуса, то высота, радиус и образующая составляют прямоугольный треугольник. Угол равный 30° лежит против катета, равного 10 см. По свойству угла в 30° (угол 30° лежит против катеты, равного половине гипотенузы), гипотенуза = 2*10 = 20 - образующая
По теореме Пифагора найдем радиус
R = =
= 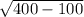 =
= 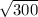
При округлении до сотых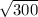 = 17,32
= 17,32
№3
Sо.с.к. = 1/2 * R * H = 1/2 * 8 * 6 = 24
ответ: 6 целых 4/7
Объяснение: рассмотрим ∆АВС. В нём известны 3 стороны, и мы можем найти используя теорему косинусов угол А:
cosA=(AB²+AC²-BC²)/2×AB×AC=
=(8²+4²-6²)/2×8×4=(64+16-36)/64=64/64=1
cosA=1
Обозначим пропорции для разных сторон как: АМ=2х, 5х, а АВ как 3у, 4у
АМ=5х; АР=3х; ВР=4х
АС=4=2х.
2х=4
х=4÷2=2; х=2
АМ=5×2=10; АМ=10
Составим уравнение по стороне АВ:
3у+4у=8
7у=8
у=8/7
АР=3у=3×8/7=24/7;. АР=24/7
Найдём РМ, используя теорему косинусов: РМ²=АР²+АМ²-2×АР×АМ×cosA=
=(24/7)²+10²-2×24/7×1=
(576/49)+100-(480/7)= здесь находим общий знаменатель и получаем:
(576/49)+(4900/49)-(3360/49)=
=2116/49; РМ=√2116/49=46/7
или 6 целых 4/7