Начертите ромб ABCD. Постройте образ этого ромба при:
а) симметрии относительно точки С;
б) симметрии относительно прямой АВ;
в) параллельном переносе на вектор АС;
г) повороте вокруг точки D на 60° по часовой стрелке.
Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через ее центр.
* Начертите два параллельных отрезка, длины которых равны. Начертите точку, являющуюся центром симметрии
(Желательно чтобы вы прикрепили фото с решением)
Объяснение: два решения, так как не знаю какую тему проходите.
1. решение.
Найдем длины сторон.
АВ =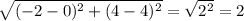
AC =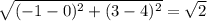
BC =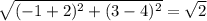
По теореме косинусов
BC²=AB²+AC²-2AC*AB*cosA и отсюда
cosA =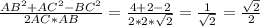
Угол А = 45°
2 решение
Найдем координаты векторов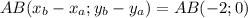
Аналогично АС(-1;-1)
Найдем модули векторов
|AB| =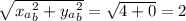
Аналогично |AC| =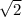
кстати, модуль вектора и есть его длина и мы эти длины уже рассчитали выше.
Скалярным произведением двух векторов является сумма произведений соответствующих координат этих векторов.
(AB*AC) = (-2*(-1)) + 0*(-1)) = 2
Тогда из формулы скалярного произведения векторов АВ и АС
cosA =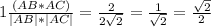
cosA = 45°
Вот вам решение :(((
В дополнение к заданным в задаче обозначениям я ввожу еще такие.
BF пересекает А в точке К. АМ = p; BN = t; NC = q; CK = x; KA = y; CF = e; FN = u; MF = f;
Ну, и АВ = с, ВС = а;
Из теорем Чевы и Ван-Обеля сразу следует
m*q*y/(p*t*x) = 1;
x/y + q/t = e/f;
y/x + p/m = n/u;
Из первого и второго равенств следует q/t = (x/y)*(p/m); и
(x/y)*(1 + p/m) = e/f;
аналогично из первого и третьего равенств p/m = (y/x)*(q/t); и
(y/x)*(1 + q/t) = n/u;
Если перемножить левые и правый части, получается
(1 + p/m)*(1 + q/t) = (e*n)/(f*u); или (c/m)*(a/t) = (e*n)/(f*u);
Пока что нигде не использовалось условие равенства углов. Это условие означает, что точки A M N C лежат на одной окружности. Отсюда сразу следует, что n*u = e*f; (произведения отрезков хорд) и m*c = t*a; (произведения отрезков секущих из точки В). Подставляя e = n*u/f; и с = a*t/m; я получаю
a^2/m^2 = n^2/f^2; или a/m = n/f;
f = n*a/m;
Между прочим, угол между f и n (угол MFA) НЕ равен углу ABC. То есть получить это равенство из подобия не получится :)