На рисунку зображено прямокутник ABCD. Знайдіть вектор 1/2DB+AB-1/2AC

Показать ответ

Ответ:

Nik10234

18.12.2022 07:21

В параллелепипеде 6 граней, - по две противоположных, которые попарно равны между собой. Естественно, их диагонали также равны.
В каждой вершине параллелепипеда сходятся смежные стороны трех граней, и их диагонали образуют треугольник. (см. рисунок вложения)
В данном случае диагонали равны 30, 40 и 70 см.
По теореме о неравенстве треугольников: длина любой стороны треугольника меньше суммы длин двух других сторон.
Здесь имеем "треугольник" и три длины, и 70=30+40.
Тогда меньшие стороны "лягут" на большую, и треугольник не получится, как и параллелепипед с такими диагоналями граней.
Не могут диагонали трех граней прямоугольного параллелепипеда иметь длины 30 см, 40 см и 70 см.
Могут ли диаганали трех граней прямоугольного параллелепипеда иметь длины 30 см , 40 см, и 70см

Могут ли диаганали трех граней прямоугольного параллелепипеда иметь длины 30 см , 40 см, и 70см

0,0(0 оценок)

Ответ:

juehxbrf

18.09.2022 06:54

Объяснение:

Задача № 1.

Дано: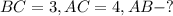 BC = 3, AC = 4, AB - ?

Решение: Так как ABC - прямоугольный треугольник, то AB можно найти по теореме Пифагора:

$AB = \sqrt{BC^{2} +AC^{2} } =\sqrt{9+16} =\sqrt{25} =5$

ответ: 5.

Задача № 2.

Дано: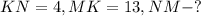 KN = 4, MK = 13, NM - ?

Решение: Так как NMK - прямоугольный треугольник, то NK можно найти по теореме Пифагора:

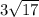
$NM = \sqrt{MK^{2} -NK^{2} } =\sqrt{169-16} =\sqrt{153} =3\sqrt{17}$

ответ: $3\sqrt{17}$

Задача № 3.

Дано: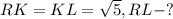 $RK=KL=\sqrt{5}, RL - ?$

Решение: так как RKL - прямоугольный треугольник, то RL найдем через теорему Пифагора:

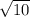
$RL = \sqrt{RK^{2} +KL^{2} } =\sqrt{5+5} =\sqrt{10}$

ответ: $\sqrt{10}$

Задача № 4.

Дано: ∠M = 30°,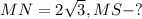 $MN=2\sqrt{3} ,MS-?$

Решение: MNS - прямоугольный треугольник:

1. Так как катет NS лежит напротив 30 градусов, то он равен половине гипотенузы:

$NS = \frac{NM}{2} =\sqrt{3}$

2. Найдем катет MS через теорему Пифагора:

$MS = \sqrt{MN^{2} -NS^{2} } =\sqrt{12-3} =\sqrt{9} =3$

ответ: 3

Задача № 5.

Дано: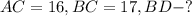 AC=16, BC=17, BD - ?

Решение: Рассмотрим треугольник BDC - прямоугольный:

$DC=\frac{AC}{2} =8$ - так как высота делит основание пополам в равнобедренном треугольнике

BD найдем по теореме Пифагора:

$BD=\sqrt{BC^{2} -DC^{2} } =\sqrt{289-64} =\sqrt{225} =15$

ответ: 15

Задача № 6.

Дано: ΔRMN - правильный,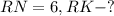 RN=6,RK-?

Решение: Рассмотрим ΔRKN - прямоугольный:

1. Высота делит основание пополам в правильном треугольнике:

NK=KM=3

2. Найдем высоту по теореме Пифагора:

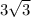
$RK=\sqrt{RN^{2} -NK^{2} } =\sqrt{36-9} =\sqrt{27} =3\sqrt{3}$

ответ: $3\sqrt{3}$

Задача № 7.

Дано: ΔMPR - правильный,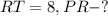 RT=8, PR -?

Решение: Рассмотрим ΔPTR - прямоугольный:

1. Высота делит основание пополам, тогда:

$PT=\frac{x}{2}$

2. Найдем PR через теорему Пифагора:

$PR^{2} =TR^{2} +PT^{2} \\x^{2} =64+\frac{x^{2} }{4} \\4x^{2} =256+x^{2} \\3x^{2} =256\\x=\sqrt{\frac{256}{3}}$

Отрицательный корень нам не подходит, так как длина отрезка не может быть отрицательной.

ответ: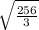 $\sqrt{\frac{256}{3}}$

Задание № 8.

Дано: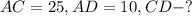 AC=25, AD=10, CD-?

Решение: Рассмотрим ΔACD - прямоугольный:

Найдем CD по теореме Пифагора:

$CD=\sqrt{AC^{2} -AD^{2} } =\sqrt{625-100} =\sqrt{525} =5\sqrt{21}$

ответ: $5\sqrt{21}$

0,0(0 оценок)

Популярные вопросы: Геометрия

uvalievnursulta2

20.09.2021 11:54

Довжина кола, описаного навколо рівнобедреного трикутника дорівнює 50п см, а бічна сторона дорівнюе 40 см.Знайти периметр та площу цього трикутника....

KristiDever

09.02.2021 13:21

Постройте треугольник АВС, если даны вершина А и прямые, на которых лежат биссектрисы углов В и С....

владимир203

05.08.2022 22:21

1. найдите углы параллелограмма авсд, если а + с = 184°. 2. в параллелограмме cdkm проведена биссектриса угла dcm, которая пересекает сторону dk в точке p. а) докажите,...

Polli200p

16.08.2022 18:33

Впрямоугольном треугольнике abc угол с=90 градусов,угол а=30 градусов, катет вс= 6 см, катет ас=8 см. чему равен периметр треугольника? , буду...

Егор1123321

07.05.2020 06:38

Являются ли углы авс и dbe вертикальными? ...

danisimokuvshn

16.08.2022 18:33

Вравнобедренном треугольнике угол при вершине 70 градусов.найти остальные углы...

vladborhovp0a44d

17.11.2020 14:01

8класс. тема параллелограмм точка к-середина стороны вс в параллелограмме авсd. точка м - середина стороны аd. докажите, что четырёхугольник аксм- парллелограмм...

помогите1170

24.09.2022 03:02

Луч с - биссектриса угла ab. луч d - биссектриса угла ac. величина угла ab равна 80 градусов. чему равна градусная мера угла bd? с решением)...

манюня5649

24.09.2022 03:02

Впрямоугольнике авсd сторона ав вдвое короче вс. найдите угол акd, где к-середина вс....

kseniasergeeva10

09.04.2021 08:39

Упражнение 174, Найдите ошибки, исправьте предложения,1. Извивающая река протекала около леса. 2. Ждя товарищана улице, мы замёрзли, 3, Вчера сестра передавала вампривет....

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку

На рисунку зображено прямокутник ABCD. Знайдіть вектор 1/2DB+AB-1/2AC​

На рисунку зображено прямокутник ABCD. Знайдіть вектор 1/2DB+AB-1/2AC