На рисунке: oa=ob; bd=ac. точка e – точка пересечения прямых ad и bc. докажите, что oe – биссектриса угла doc. указание: для решения необходимо воспользоваться тремя различными признаками равенства для различных пар треугольников.
Значит сначала мы должны найти площадь основания пирамиды, а затем площадь боковой поверхности пирамиды.
В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому (см²).
Площадь боковой поверхности правильной четырёхугольной пирамиды - полупроизведение периметра основания на апофему.
Значит нам нужно сначала найти апофему нашей пирамиды.
1 правило: Апофема делит сторону основания пополам.2 правило: Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды.
Объяснение 1 правила: из этого следует, что апофема делит сторону основания так, что (см).
Объяснение 2 правила: внутри нашей пирамиды образовался прямоугольный , где - катет прямоугольного тр-ка (высота пирамиды); - катет прямоугольного тр-ка; - гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что (см).
Так как апофема нашей пирамиды является ещё и гипотенузой прямоугольного , то мы сможем найти её величину по т.Пифагора:
(см).
Теперь найдём периметр основания (квадрата):
(см).
Затем найдём площадь боковой поверхности:
(см²).
Остаётся найти ответ на вопрос: "Чему равна площадь полной поверхности пирамиды?"
Задача имеет два решения. 1) Дан внешний угол при вершине равнобедренного треугольника. Тогда сумма двух углов при основании равна 130·. Но углы при основании равны, значит каждый из них равен 130 : 2=65° Третий угол при вершине будет смежным с углом в 130°. Третий угол треугольника равен 180-130=50°. ответ: 50°; 65°; 65°. 2) Если дан внешний угол при основании, то углы треугольника при основании равны будут по 50° , то есть 180-130=50. Угол при вершине равнобедренного треугольника равен 80°. ответ: 80°; 50°; 50°.
Правильная четырёхугольная пирамида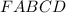 .
.
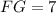 (см).
(см).
Найти: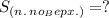 (см²).
(см²).
Решение:Значит сначала мы должны найти площадь основания пирамиды, а затем площадь боковой поверхности пирамиды.
В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому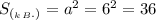 (см²).
(см²).
Площадь боковой поверхности правильной четырёхугольной пирамиды - полупроизведение периметра основания на апофему.
Значит нам нужно сначала найти апофему нашей пирамиды.
1 правило: Апофема делит сторону основания пополам.2 правило: Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды.Объяснение 1 правила: из этого следует, что апофема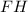 делит сторону основания
делит сторону основания 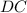 так, что
так, что 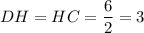 (см).
(см).
Объяснение 2 правила: внутри нашей пирамиды образовался прямоугольный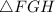 , где
, где 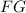 - катет прямоугольного тр-ка (высота пирамиды);
- катет прямоугольного тр-ка (высота пирамиды); 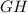 - катет прямоугольного тр-ка;
- катет прямоугольного тр-ка; 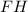 - гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что
- гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что 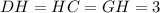 (см).
(см).
Так как апофема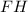 нашей пирамиды является ещё и гипотенузой прямоугольного
нашей пирамиды является ещё и гипотенузой прямоугольного 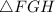 , то мы сможем найти её величину по т.Пифагора:
, то мы сможем найти её величину по т.Пифагора:
Теперь найдём периметр основания (квадрата):
Затем найдём площадь боковой поверхности:
Остаётся найти ответ на вопрос: "Чему равна площадь полной поверхности пирамиды?"
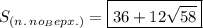 (см²).
(см²).
ответ:1) Дан внешний угол при вершине равнобедренного треугольника. Тогда сумма двух углов при основании равна 130·. Но углы при основании равны, значит каждый из них равен 130 : 2=65° Третий угол при вершине будет смежным с углом в 130°. Третий угол треугольника равен 180-130=50°. ответ: 50°; 65°; 65°.
2) Если дан внешний угол при основании, то углы треугольника при основании равны будут по 50° , то есть 180-130=50.
Угол при вершине равнобедренного треугольника равен 80°. ответ: 80°; 50°; 50°.