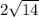Итак, чертеж к задаче прикреплен снизу. Так как треугольник является прямоугольным, то в нем действует теорема Пифагора: квадрат гипотенузы равен сумме квадратов двух катетов прямоугольного треугольника. В алгебраической форме эту теорему записывают так:
c^2 = a^2 + b^2 (^2 - вторая степень числа)
Из этой формулы выразим a^2, т.к. именно катет a нужно найти(см. чертеж внизу)
a^2 = c^2 - b^2
Но мы то выразили только КВАДРАТ стороны, а не саму сторону. То есть, чтобы найти саму сторону, нам нужно извлечь корень квадратный из выражения c^2 - b^2
В итоге, вычислив значение а(см. картинку внизу), мы получаем ответ
Угол между образующей конуса и плоскостью основания равен углу между образующей и радиусом основания, проведенного к данной образующей. Площадь боковой поверхности конуса: pi*R*l, площадь основания - pi*R^2. Поскольку площадь боковой поверхности в два раза больше площади основания, то pi*R*l = 2*pi*R^2. упрощаем уравнение: l = 2R. Из рисунка CB = 2OB. Из прямоугольного треугольника COB: угол, который лежит против катета, который в два раза меньше гипотенузы, равен 30 градусов. OB - катет, CB - гипотенуза, следовательно, угол BOC = 30 градусов. Искомый угол CBO = 90 - 30 = 60 градусов.
Объяснение:
Итак, чертеж к задаче прикреплен снизу. Так как треугольник является прямоугольным, то в нем действует теорема Пифагора: квадрат гипотенузы равен сумме квадратов двух катетов прямоугольного треугольника. В алгебраической форме эту теорему записывают так:
c^2 = a^2 + b^2 (^2 - вторая степень числа)
Из этой формулы выразим a^2, т.к. именно катет a нужно найти(см. чертеж внизу)
a^2 = c^2 - b^2
Но мы то выразили только КВАДРАТ стороны, а не саму сторону. То есть, чтобы найти саму сторону, нам нужно извлечь корень квадратный из выражения c^2 - b^2
В итоге, вычислив значение а(см. картинку внизу), мы получаем ответ