На малюнку A1B1 || A2B2 || A3B3, А1А2 = 3 см, ОА1 = 9 см. Знайдіть ОВ1, якщо ОВ2 = 40 см

Показать ответ

Ответ:

Taksa64

02.04.2022 21:18

Дано :

ΔАВС ~ ΔA₁В₁С₁.

Отношение сходственных сторон = $\frac{6}{5}$ .

S(ΔАВС) = S(ΔА₁В₁С₁) + 77 (см²).

Найти :

S(ΔАВС) = ?

S(ΔА₁В₁С₁) = ?

Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.

Отсюда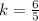 $k = \frac{6}{5}$ .

Так как k > 1, то в числителе стоит бо́льший треугольник.

Площади подобных треугольников относятся как квадрат коэффициента подобия.

Пусть S(ΔА₁В₁С₁) = х, тогда S(ΔАВС) = х + 77 (см²) (так как площадь ΔАВС больше площади ΔА₁В₁С₁, то он, как раз таки, и есть бо́льший треугольник).

Составим уравнение -

$\frac{S(\triangle ABC)}{S(\trianle A_{1} B_{1}C_{1})} = k^{2}\\\\ \frac{x + 77}{x} = (\frac{6}{5})^{2}\\\\\frac{x + 77}{x} = \frac{36}{25}\\\\25*(x + 77) = 36x\\\\25x + 1925 = 36x\\\\25x - 36x = -1925\\\\-11x = -1925\\\\ \boxed{x = 175}$

S(ΔА₁В₁С₁) = x = 175 (cм²)

S(ΔАВС) = х + 77 (см²) = 175 (см²) + 77 (см²) = 252 (см²).

252 (см²), 175 (см²).

Треугольники авс и а1в1с1 подобны, и их сходственные стороны относятся как 6: 5. площадь треугольник

0,0(0 оценок)

Ответ:

goshaaaAa

08.02.2021 22:48

Т.к. АВС- равнобедренный треугольник (по условию), то АС=ВС, следовательно АС=ВС=СК=СМ
Рассмотрим треугольник АВС- он прямоугольный, равнобедренный, следовательно угол САВ= углу АВС=45градусам (сумма углов треугольника равна 180 градусам)
Аналогично в треугольниках АМС, МСК, КСВ, следовательно углы МАС= САВ= АВС= СВК= ВКС= СКМ= 45 градусов, следовательно угол А= углу В= углу К= углу М= 90 градусов, следовательно МАВК- прямоугольник.
Рассмотрим тоеугольники АВС и ВКС. Они прямоугольные и равны по катету и острому углу (или по 2 катетам), следовательно АВ=ВК=5см,следовательно МАВК- квадрат.
Площадь квадрата = а в квадрате, следовательно площадь АВКМ равна 5*5=25см квадратных.

0,0(0 оценок)

Популярные вопросы: Геометрия