На фигуре треугольник abc с центроидом g, дано e делит сторону ac на два равных отрезка,fe||bc и площадь треугольника efg =5. надо найти площать треугольника abc. .это 5

Поскольку  ab||mn то  ∠abm=∠bmn, как   поскольку bn=nm то  ∠bmn=∠mbn, как углы при основании из этого всего ∠mbn=∠bmn, тоэсть  bm - бисектриса, которая в равнобедренном триугольнике есть и медианой  ⇒  am=mc

ответ  

ответ разместил: Гость

Решение и чертеж в приложении. ответ : r авс =5

ответ  

ответ разместил: Гость

По теореме: если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон. следовательно, не может.

ответ  

ответ разместил: Гость

3. -3

Объяснение:

Точки A, B, C, D не лежат в одной плоскости. К и M - точки пересечения медиан треугольников АCD и BCD соответственно. Докажите, что четырехугольник АКМВ является трапецией. Вычислите длину отрезка КМ, если AB 27 CM.  Сделайте с рисунком.

Объяснение:

1) Пусть медиана АК , ΔСDA , пересечет сторону АD в точке О, СО=ОD.

В ΔСDB соединим О с В, ОВ- медиана , М-точка пересечения медиан.

По т. о точке пересечения медиан имеем

ΔОМК подобен ΔОВА по 2-м пропорциональным сторонам и равному углу между этими сторонами :∠О-общий,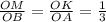 ⇒соответственные углы равны ∠ОКМ=∠ОАВ , при секущей ОА ⇒ МК║АВ по признаку параллельности прямых.

У четырехугольника АКМВ 2 стороны параллельны ⇒ это трапеция.

2) Т.к. ΔОМК подобен ΔОВА то сходственные стороны пропорциональны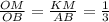    или KM=27*1:3=9 (см) .