«Метод координат в куб. Найдите вектор, равный (AA1 ) ⃗+ (B1 C) ⃗-(C1 D1 ) ⃗ .
2. Даны координаты точек: A(-3;2;-1),B(2;-1;-3),C(1;-4;3),D(-1;2;-2) .
Найдите |2(AB) ⃗+3(CD) ⃗ |
3. Даны координаты точек: C(3;-2;1),D(-1;2;1),M(2;-3;3),N(-1;1;-2) .
Найдите косинус угла между векторами
(CD) ⃗ и (MN) ⃗.
4. При каком значении p векторы a ⃗{6-p;p;2} и b ⃗{-3;5+5p;-9} перпендикулярны?
5. Длина ребра куба ABCDA1 B1 C1 D1 равна 2. Вычислите скалярное произведение векторов
а) (AB1 ) ⃗ и (CC1 ) ⃗; б) (AB1 ) ⃗ и (CD1 ) ⃗.
20 ед. изм.
Объяснение:
Тангенс угла Т=3, значит РН/ТН=15/5=3, ТН=5
КН=МР=15
КТ=15+5=20.
Вариант 1
№1. Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.
Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора: BC =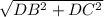 =
= 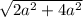 =
= 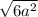 =
= 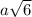
№2. Пусть D - данная точка. DB и DC - наклонные. Проведем AD — перпендикуляр к плоскости α. Тогда АВ и АС — проекции наклонных на плоскость α. Тогда ΔABD и ΔACD — прямоугольные, равнобедренные. Так что АВ = АC = AD = а.
DC = DB = a : sin45 =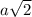
Так что ΔBDC — равнобедренный, а поскольку ∠BDC = 60°, то значит треугольник BDC — равносторонний, т.е.
DB = DC = BC =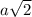
(Дальше долко)