Во-первых, рассмотрим ΔAFB и ΔEFD.
1) ∠AFB = ∠EFD ( тк вертик )
2)∠EDF = ∠FAB (тк накрест лежащие углы при ED ║ AB и секущей AD )
Значит, ΔAFB ≅ ΔEFD ( по двум углам ).
во-вторых, площади подобный треугольников относятся как квадрат коэффициента подобия, DE - средняя линия треугольника. Значит = .
Найдём площадь, Δ AFB / ΔEFD = 1/1/2^2 = 0, 25 см².
ответ: SΔDEF = 0, 25 см²
Во-первых, рассмотрим ΔAFB и ΔEFD.
1) ∠AFB = ∠EFD ( тк вертик )
2)∠EDF = ∠FAB (тк накрест лежащие углы при ED ║ AB и секущей AD )
Значит, ΔAFB ≅ ΔEFD ( по двум углам ).
во-вторых, площади подобный треугольников относятся как квадрат коэффициента подобия, DE - средняя линия треугольника. Значит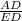 =
= 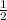 .
.
Найдём площадь, Δ AFB / ΔEFD = 1/1/2^2 = 0, 25 см².
ответ: SΔDEF = 0, 25 см²