Лежит ли точка А (2; –1) на окружности, заданной уравнением (х – 2)² + (у – 3)² = 25? 2. Напишите уравнение окружности, если ее центр – точка (4; 5), а радиус равен 3. 3. Напишите уравнение прямой, проходящей через точку М (3; –2) и параллельной оси ординат. 4. Напишите уравнение окружности с центром в начале координат, если она проходит через точку С (–2; 3). 5. Напишите уравнение прямой, проходящей через две точки М (–2; –1) и N (3; 1). 6. Найдите длину вектора ā(–12; 5). 7. Найдите координаты середины отрезка PQ, если P (5; –3); Q (3; –7). 8. Найдите координаты вектора , если А (2; –5), В (–3; 4).
ответ: Диаметр самая длинная хорда в окружности, запомните это дети! И ешьте манную кашу!
Объяснение:
АО = ОВ = 5, тогда радиус равен АО = ОС = 10. Отрезок ВС = 15.
Если хорда пересекается диаметром перпендикулярно, то хорда делится пополам, поэтому DB=BE.
Хорды в точке пересечения делятся на отрезки так, что произведение отрезков одной хорды равно произведению отрезков второй.
То есть, DB*DE = AB*BC отсюда DC²= 5*15 = 75, DC = 5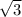
По теореме Пифагора, DC² = DB²+BC². И подставив значения найдем, что DC = 10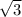
1. 12 * 7 = 84 см"
2. 24 см
3.49√2 см
4. -----------
5.24√2 см²
Объяснение:
1. Тут и так понятно)
2. Высота поделила основу пополам,тем самым поделив треугольник на 2 маленьких.По теореме Пифагора квадрат гипотенузы = сумме квадратов катетов. Найдём катет( половину основы треугольника).
225 = 81 +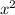
х =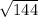
= 12 см
Теперь узнаем длинну основы: 12 +12 = 24 см
3.Площадь ромба через его сторону и угол
S = a²·sin(β) = (7√2)²·sin(135°) = 49*2 * 1/√2 = 49√2 см
4. Не знаю, прости((((
5.Дано: трапеція КМРТ, МР=7 см, КТ=9 см, ∠Т=45°.
Проведемо висоту РН. Розглянемо ΔРТН - прямокутний.
∠Т=45°, тоді ∠ТРН=90-45=45°, тобто ΔРТН - рівнобедрений.
Нехай РН=ТН=х см, тоді за теоремою Піфагора
х²+х²=6²; 2х²=36; х²=18; х=√18=3√2; РН=3√2 см.
S=(МР+КТ):2*3√2=(7+9)/2*3√2=24√2 см²