Кут між площинами трикутників abc acf дорівнює 30 ° трикутник abc рівносторонній ab=10 см трикутник acf рівнобндрений af=cf= корінь 194 см знайти довжину відрізка bf​

5.2.  Если прямая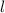    перпендикулярна двум пересекающимся прямым (АВ и АС) , лежащим в одной плоскости ( пл. треугольника АВС) , то эта прямая  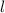  перпендикулярна самой плоскости ( пл. ΔАВС).

в) Прямая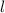    перпендикулярна плоскости треугольника АВС.

5.3.  Так как КО⊥ АВСД ( плоскости параллелограмма АВСД) , то эта прямая перпендикулярна ЛЮБОЙ прямой, лежащей в плоскости АВСД. Значит, КО⊥АВ , КО⊥ВС , КО⊥АД , КО⊥СД , КО⊥АС , КО⊥ВД ,...

5.4.  МВ⊥пл ΔАВС  ⇒  МВ перпендикулярна ЛЮБОЙ прямой, лежащей в этой плоскости АВС, в том числе МВ⊥ВХ ( Х∈АС⊂ΔАВС ) ⇒

∠МВХ=90°  и  ΔМВХ - прямоугольный .

Cм. рисунки.

лина меньшей диагонали д будет зависеть от меньшего угла параллелограмма, который равен: <А = (180° - 120°) = 60°., и от двух его сторон а и в. Используем формулу определения любой  стороны в треугольнике с косинуса угла, и двух других сторон, где а и в - стороны параллелограмма. (Стороны а, в, и д составляют треугольник с углом А = 60°).

д^2 = а^2 + в^2 + 2 а * в * соs < А = 3^2 + 4^2 + 2 * 3 * 4 * соs (60°) = 9 + 16 + 24 * 1/2 = 25 + 12 = 37 (см^2).

Меньшая диагональ д равна:

д = √(37) см.

Объяснение:

вроде так понела:3