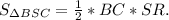SR - апофема пирамиды. Площадь боковой поверхности состоит из суммы площадей 3-х равных треугольников, которые являются боковыми гранями пирамиды. То есть . В данном случае речь идет о треугольнике BSC. так как площади треугольников равны, то можно записать в следующем виде Делим обе части на 3. . Так как треугольник BSR - равнобедренный (из того, что пирамида -правильная), то его площадь равна произведению половины основания BC на высоту SR. Так как пирамида правильная, то AB=BC.
. Делим обе части уравнения на 4. , то есть SR=21.
Если прямая параллельна хотя бы одной прямой лежащей в плоскости то она либо параллельная самой плоскости либо принадлежит ей.
Рассмотрим тр. AMD и BMC
A1D1 - сред. линия тр. AMD, не принадлежит ABCD, A1D1 || AD
B1C1 - сред. линия тр. BMC, не принадлежит ABCD, B1C1 || BC
по условию BC||AD ⇒ A1D1 || B1C1
ч.т.д.
AD:BC=5:3
KL - ср. линия трап. = 16 см
A1D1 - ?
B1C1 - ?
Введем переменную x ⇒ AD=5x, BC=3x
Тогда по формуле средней линии трапеции:
16=(5x+3x)/2
32=8x
x=4
AD=5*4=20 см
BC=3*4=12 см
Тогда:
A1D1=1/2*AD=1/2*20=10 см
B1C1=1/2*BC=1/2*12=6 см
SR - апофема пирамиды. Площадь боковой поверхности состоит из суммы площадей 3-х равных треугольников, которые являются боковыми гранями пирамиды. То есть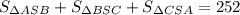
. В данном случае речь идет о треугольнике BSC. так как площади треугольников равны, то можно записать в следующем виде 
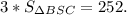Делим обе части на 3. 
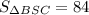. Так как треугольник BSR - равнобедренный (из того, что пирамида -правильная), то его площадь равна произведению половины основания BC на высоту SR. Так как пирамида правильная, то AB=BC. 