«Коло і круг»

2 варіант
1.Знайти діаметр кола, якщо радіус дорівнює 3,6 см
2. Побудувати коло, радіус якого дорівнює 40 мм. Провести в ньому радіус DB, діаметр CE, хорду LK. З точки F, що не належить колу провести дві дотичних FM і FA, одна з яких дорівнює 3 см. Яку довжину буде мати друга дотична? 3. Визначити взаємне розміщення двох кіл радіусів 2 см і 3 см, якщо відстань між їх центрами дорівнює 5 см.
4. Два кола мають внутрішній дотик. Відстань між їх центрами дорівнює 18 см. Знайти радіуси кіл, якщо вони відносяться як 7 : 5.
5. Відрізки ОС і ОD – радіуси кола з центром О. Знайти кути трикутника OCD, якщо ∠ CОD = 108°.
6. У колі з центром О провели хорду АР, довжина якої 4 см. Знайти радіус кола, якщо периметр трикутника OРА дорівнює 15 см хоть одним заданием буду благодарен

угол D=60°, угол С=90°, угол А=30°, угол С=30° и угол В=120°

Объяснение:

Проведенная диагональ АС делит этот параллелограмм АВСD на два треугольника: равнобедренный треугольник АВС и прямоугольный треугольник АСD.

Так как АСD прямоугольный треугольник, то угол С=90°.Итак у нас есть угол D(60°) и угол С(90°), находим угол А. Так как сумма углов треугольника равна 180°, получаем: 180°-уголD(60°)-уголС(90°)=30° -угол А. Итак мы нашли все углы прямоугольного треугольника АСD.

Перейдем к треугольнику АВС. Так как угол А=30°, то и угол С тоже будет 30° так как в равнобедренном треугольнике углы при основании равны. Получаем что угол А=30° и угол С=30°. И так как сумма углов треугольника равна 180°, получаем: 180°-уголА(30°)-уголС(30°) =120° -угол В.

Задача решена.

A)Допустим, это не так. Тогда точки A₁0₁B₁0₂ лежат в одной плоскости. Тогда в ней же лежат прямые, проходящие через O₁;O₂ параллельные A₁B₁ или, что то же самое, параллельные CD В частности, там лежат середины ребер AD и DD₁ ни вместе с A₁ задают плоскость грани куба AA₁D₁D, в которой не лежит B₁. Противоречие.

б)Введем координаты с началом в точке A и с осями x,y,z, направленными вдоль прямых AD,AB,AA₁ соответственно. Тогда координаты точек будут такими: A₁(0,0,2),B₁(0,2,2),O₁(1,1,0),O₂(2,1,1). Если отложить вектор A₁B₁ от точки B₁, то его конец T будет иметь координаты (1,3,0). Написав уравнение плоскости, проходящей через B₁,O₂,T, получим x+y+z-4=0. Тогда расстояние от точки (0;0;2) до этой плоскости составит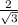

Объяснение: