Кола з центрами в точках O1 і O2 дотикається зовнішнім чином у точці A.Знайдіть O2A якщо O1O2=10см, O2A =6см Зделайте

Кола з центрами в точках O1 і O2 дотикається зовнішнім чином у точці A.Знайдіть O2A якщо O1O2=10см,

Показать ответ

Ответ:

nastushka208

07.07.2021 21:13

Формулы:

Обозначим, что X - угол А; Y - угол В (нам уг. С не нужен).

sinX =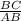 $\frac{BC}{AB}$

cosX =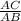 $\frac{AC}{AB}$

tgX =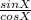 $\frac{sinX}{cosX}$

Также и с "Y". Только подставлять другие стороны.

AC = 15, BC = 8, AB - ?

Найдем АВ по т. Пифагора:

$AB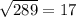^{2} = AC^{2} + BC^{2}$ = 225 + 64 = 289

AB = $\sqrt{289} = 17$

Ищем косинусы,синусы и тангенсы.

sinX = 8 / 17 =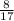 $\frac{8}{17}$

cosX =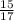 $\frac{15}{17}$

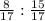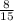
tgX = $\frac{8}{17} : \frac{15}{17}$ = $\frac{8}{15}$

...

sinY =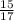 $\frac{15}{17}$

cosY =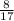 $\frac{8}{17}$

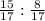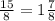
tgY = $\frac{15}{17} : \frac{8}{17}$ = \ $\frac{15}{8} = 1\frac{7}{8}$

P.S. за 2 месяца я немного забыл, что синусы вроде так ищутся. Я впервые сталкиваюсь, что у меня вот такие дроби получаются. Если будет ошибка - уведомляй. Рисунок я добавил, чтобы не запутаться.

Помигите . в треугольнике авс угол с=90 градусов. ас=15см, вс=8 см. найдите sin а, cos a, tg а, sin

0,0(0 оценок)

Ответ:

медвва

04.12.2022 17:14

Точку из которой проведены наклонные обозначим К. Опусти из неё на плоскость перпендикуляр КС. Точки пересечения наклонных с плоскостью А и В. Получим отрезки наклонных АК, ВК и их проекции на плоскость АС и ВС. Треуольники АКС и ВКС равны как прямоугольные по острому углу и катету (Ф и КС). Тогда их строны АК и ВК равны. Обозначим их Х. Соединим А и В. Угол АСВ по условию равен В. Углы КАС и КВС равны Ф. АС=ВС=Х*cos Ф. По теореме косинусов АВ квадрат=(Х*cos Ф)квадрат +(Х*cos Ф)квадрат -2*Х*cos Ф*Х*cosФ*cosВ. Это в треугольнике АСВ. В треугольнике АКВ аналогично АВ квадрат=Х квадрат+Хквадрат-2*Х*Х* cos K. Приравниваем полученные выражения и получим cos K=1-(cos Ф)квадрат*(1-cos В). Где К искомый угол АКВ между наклонными

0,0(0 оценок)

Популярные вопросы: Геометрия