К окружности проведены касательная и секущая, - вопрос №13579859 от andrii213 25.03.2023 23:51

Question

Геометрия: К окружности проведены касательная и секущая, проходящая через центр окружности. Длина касательной в два раза меньше длины секущей. Найдите отношение длины касательной к длине радиуса.​

andrii213 · Answer

К окружности проведены касательная и секущая, проходящая через центр окружности. Длина касательной в два раза меньше длины секущей. Найдите отношение длины касательной к длине радиуса.

Объяснение:

По условию 2АМ=МС. Пусть радиус окружности r. Нужно найти $\frac{AM}{r}$ .

" Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC2 = MA•MB. "

АМ²=МВ*МС , но длина отрезка МВ=МС-2r ,

АМ²=( МС-2r)*2АМ |: АМ , МС=2АМ ,

АМ=(2АМ-2r)*2,

3АМ=4r ⇒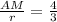 $\frac{AM}{r} =\frac{4}{3}$ .

К окружности проведены касательная и секущая, проходящая через центр окружности. Длина касательной в