Наш треугольник прямоугольный и один из углов 45°, значит третий угол треугольника равен 90° - 45° = 45°.
Получается, что в треугольнике 2 равных угла по 45°, следовательно данный треугольник равнобедренный, следовательно катеты и равны, то есть второй катет тоже 8 см.
Гипотенузу находим по теореме Пифагора:
(см)
P.S
Признак равнобедренного треугольника: если два угла треугольника равны, то такой треугольник равнобедренный
Примем дугу ЕКН за х
Тогда дуга ЕАН=х+90
В сумме эти две дуги составляют 360 градусов.
х+х+90=360
2х=360-90
2х=270
х=135
х+90=135+90=225
Вписанный угол ЕАН опирается на дугу, равную 135 градусов. Он равен половине центрального угла, опирающегося на ту же дугу
135:2=67,5
Вписанный угол ЕКН опирается на дугу, равную 225 градусов.
Он равен половине центрального угла, опирающегося на ту же дугу и равен
225:2=112, 5
Вписанный угол ЕКА опирается на дугу 180 градусов, и равен половине центрального угла 180 градусов
180:2=90
угол ЕАН=67,5ᵒ
угол ЕКН=112, 5ᵒ
угол ЕКА=90ᵒ
8см,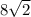
см
Объяснение:
Наш треугольник прямоугольный и один из углов 45°, значит третий угол треугольника равен 90° - 45° = 45°.
Получается, что в треугольнике 2 равных угла по 45°, следовательно данный треугольник равнобедренный, следовательно катеты
и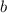 
равны, то есть второй катет тоже 8 см.
Гипотенузу
находим по теореме Пифагора:
P.S
Признак равнобедренного треугольника: если два угла треугольника равны, то такой треугольник равнобедренный
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов