В сечении получается равнобокая трапеция.
Вершины верхнего основания этой трапеции лежат на серединах боковых рёбер.
Находим длину бокового ребра L.
L = √(H² + (d/2)²) = √(8² + (4√2)²) = √(64 + 32) = √96 = 4√6 см.
Находим длину боковой стороны трапеции "в".
Для этого находим косинус угла при основании боковой грани.
cos A = (a/2)/L = 4/(4√6) = 1/√6 = √6/6.
Тогда в = √64 + 24 - 2*8*2√6*(√6/6)) = √56 = 2√14 см.
Теперь можно определить высоту трапеции h.
h = √(в² - ((8 - 4)/2)²) = √(56 - 4) = √52 = 2 √13 см.
Получаем ответ: S = h*lср = 2√13*6 = 12√13 см².
1) ; 2) Величина острого (наименьшего) угла.
1) Начертим две пересекающие прямые. Обозначим их буквами и
При их пересечении, образовался угол в
Пусть
как вертикальные.
и - смежные
2) Угол между двумя пересекающимися прямыми - это величина наименьшего угла между двумя пересекающимися прямыми.
Обозначим две пересекающиеся прямые буквами и
При пересечении произвольных прямых, образуются 4 угла: 2 равных тупых угла и 2 равных острых угла (они равны, как вертикальные).
В данном случае наименьший угол - это величина острого угла, так как величина острого угла меньше тупого.
=============================================================
Но если прямые перпендикулярные (прямые, при пересечении которых образуются 4 прямых угла), то наименьший угол - это величина прямого. Но в данной задаче этого не уточняется, поэтому верный ответ - величина острого угла.
В сечении получается равнобокая трапеция.
Вершины верхнего основания этой трапеции лежат на серединах боковых рёбер.
Находим длину бокового ребра L.
L = √(H² + (d/2)²) = √(8² + (4√2)²) = √(64 + 32) = √96 = 4√6 см.
Находим длину боковой стороны трапеции "в".
Для этого находим косинус угла при основании боковой грани.
cos A = (a/2)/L = 4/(4√6) = 1/√6 = √6/6.
Тогда в = √64 + 24 - 2*8*2√6*(√6/6)) = √56 = 2√14 см.
Теперь можно определить высоту трапеции h.
h = √(в² - ((8 - 4)/2)²) = √(56 - 4) = √52 = 2 √13 см.
Получаем ответ: S = h*lср = 2√13*6 = 12√13 см².
1)
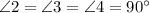; 2) Величина острого (наименьшего) угла.
Объяснение:1) Начертим две пересекающие прямые. Обозначим их буквами
и 
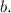
При их пересечении, образовался угол в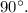
Пусть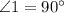
Вертикальные углы равны.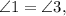
как вертикальные.
Сумма смежных углов равна2) Угол между двумя пересекающимися прямыми - это величина наименьшего угла между двумя пересекающимися прямыми.
Обозначим две пересекающиеся прямые буквами
и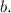 
При пересечении произвольных прямых, образуются 4 угла: 2 равных тупых угла и 2 равных острых угла (они равны, как вертикальные).
В данном случае наименьший угол - это величина острого угла, так как величина острого угла меньше тупого.
=============================================================
Но если прямые перпендикулярные (прямые, при пересечении которых образуются 4 прямых угла), то наименьший угол - это величина прямого. Но в данной задаче этого не уточняется, поэтому верный ответ - величина острого угла.