Https://minhag.ucsc.edu/node/6594
https://minhag.ucsc.edu/node/6596
https://minhag.ucsc.edu/node/6597
https://minhag.ucsc.edu/node/6595
https://minhag.ucsc.edu/node/6598
https://minhag.ucsc.edu/node/6599
https://minhag.ucsc.edu/node/6600
https://minhag.ucsc.edu/node/6601
https://minhag.ucsc.edu/node/6602
https://minhag.ucsc.edu/node/6603
https://minhag.ucsc.edu/node/6604
https://minhag.ucsc.edu/node/6613
https://minhag.ucsc.edu/node/6605
https://minhag.ucsc.edu/node/6606
https://minhag.ucsc.edu/node/6607
https://minhag.ucsc.edu/node/6608
https://minhag.ucsc.edu/node/6609
https://minhag.ucsc.edu/node/6610
https://minhag.ucsc.edu/node/6611
https://minhag.ucsc.edu/node/6612
а) Доказано; б) 36
Объяснение:
а)
Обратимся к первому рисунку. Пусть ∠AOB=∠COD=ω. Тогда ∠BAO=∠ABO=∠OCD=∠ODC=α (AO=OB=R и CO=OD=R => треугольники ABO и COD равнобедренные, в которых угол против основания общий, а =>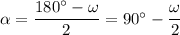
). ΔAOD равнобедренный (AO=OD=R) => ∠OAD=∠ODA=β. Аналогично ∠OBC=∠OCB=γ. Т.к. четырехугольник вписан в окружность, то ∠BAD+∠BCD=180°. Значит: 
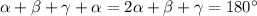. ∠BAD+∠ABC=
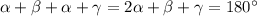. Получили, что 
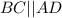, т.к. внутренние односторонние углы при этих прямых и секущей AB в сумме дают 180°. Поскольку AD≠BC (по условию AD=2BC), четырехугольник трапеция, а не параллелограмм, а так как она вписана в окружность, то равнобедренная. Доказано.
Заметим, что центр описанной около четырехугольника окружности может лежать вне него. Тогда доказательство будет отличаться. Начиная с этого момента забудем о тех обозначениях, которые были введены для доказательства первого случая. Обратимся ко второму рисунку. Заметим, что ∠ABC=∠BCD=α, так как AO=OB=R и CO=OD=R => треугольники ABO и COD равнобедренные, в которых угол против основания общий, а =>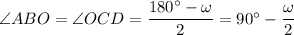
(здесь ∠AOB=∠COD=ω) и ∠OBC=∠BCO, так как это углы при основании равнобедренного треугольника BOC (OB=OC=R). Пусть ∠BAD=β. Тогда 
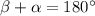(так как четырехугольник вписанный). Но 
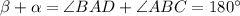. Значит 
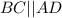, т.к. внутренние односторонние углы при этих прямых и секущей AB в сумме дают 180°. Поскольку AD≠BC (по условию AD=2BC), четырехугольник трапеция, а не параллелограмм, а так как она вписана в окружность, то равнобедренная. Доказано.
б)
Решим задачу для 1-ого случая:
Пусть EG - расстояние между прямыми BC и AD. Т.к. BC||AD, то EG=6. Заметим, что треугольники BOC и AOD равновеликие.
Докажем это:
Пусть ∠BOC=α. Тогда (так как ∠AOB=∠COD=90°, а => ∠BOC+∠AOD=360°-90°-90°=180°) ∠AOD=180°-α.
Получим:
Запишем их площади через формулу про основание и высоту:
Из условия следует, что AD=2BC.
Тогда:
Знаем, что:
Тогда:
Поскольку треугольники BOC и AOD равнобедренные, то OG и OE не только их высоты, но и медианы соответственно, а значит BG=BC/2 и AE=AD/2.
Тогда из прямоугольных треугольников BOG и AOE по теореме Пифагора найдем BC и AD:
По условию AD=2BC.
Значит:
Теперь находим BC и AD:
Теперь можно без труда найти площадь трапеции:
Получили, что площадь трапеции ABCD равна 36.
Задача решена!
(Для второго случая решить пункт б) невозможно, так как дуга AB + дуга CD по условию должны давать 180°, что невозможно для данного случая)
(см. объяснение)
Объяснение:
1)
Тебя просят найти боковую сторону. У тебя есть ее часть. Значит найти нужно другую ее часть.
Пусть x - неизвестная часть боковой стороны.
Тогда высота треугольника равна:
И соответственно основание равно:
С другой стороны основание равно:
Получили уравнение:
Откуда находим x=1.
Тогда вся сторона равна 8.
2)
Вспомним формулу:
где a и b - катеты треугольника BDC, а c - гипотенуза.
Найдем a+b:
Вспомним формулу:
Это площадь треугольника BDC.
Тогда площадь ABC:
Подставим в формулу значения из дано и получим ответ: