2. 1) MY=2 см ( точка Y лежить зліва від точки М на відстані 2 см)
KY=18 см
DY=10 см
2) MY=18 см
KY=2 см ( точка Y лежить зправа від точки К на відстані 2 см)
DY=10 см
Объяснение:
1. Довжина кожного утвореного відрізка дорівнює а
тоді середина такого відрізку дорівнює а
Знаходимо відстань між серединами крайніх відрізків:
L = а+а+а+а+а = а+а = а+а = а = 0,8а
2. Оскыльки МY + KY=16 см, якщо Y лежить на даному выдрізку, а відстань від кінця до середини відрізку 8 смб тоді точка Y лежить на прямій за відрізком
Є 2 випадки, що задовільняють умову задачі:
1) MY=2 см ( точка Y лежить зліва від точки М на відстані 2 см)
KY=18 см
DY=10 см
2) MY=18 см
KY=2 см ( точка Y лежить зправа від точки К на відстані 2 см)
Дано: АВСD - трапеция, ВD⊥АВ, АС⊥СD, ВС=10 см, АD=26 см.
Доказать, что АВ=СD. Найти S(АВСD).
По условию ∠АВD=∠АСD=90°; значит, эти углы опираются на диаметр АD окружности, которую можно описать вокруг трапеции АВСD. Поскольку окружность можно описать только вокруг равнобедренной трапеции, то трапеция АВСD - равнобедренная.
Чтобы найти площадь трапеции, проведем высоты ВН и СК. Тогда
ВС=КН=10 см, АН=КD=(26-10):2=8 см.
Найдем СК из ΔАСD, где СК=√(АК*КD)=√((10+8)*8)=√144=12 см.
1. L = 0,8а
2. 1) MY=2 см ( точка Y лежить зліва від точки М на відстані 2 см)
KY=18 см
DY=10 см
2) MY=18 см
KY=2 см ( точка Y лежить зправа від точки К на відстані 2 см)
DY=10 см
Объяснение:
1. Довжина кожного утвореного відрізка дорівнює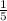
а
тоді середина такого відрізку дорівнює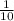
а
Знаходимо відстань між серединами крайніх відрізків:
L =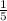
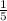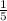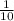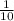а+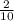
а+
а+
а+
а =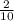 
а+
а =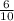 
а+
а =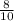 
а = 0,8а
2. Оскыльки МY + KY=16 см, якщо Y лежить на даному выдрізку, а відстань від кінця до середини відрізку 8 смб тоді точка Y лежить на прямій за відрізком
Є 2 випадки, що задовільняють умову задачі:
1) MY=2 см ( точка Y лежить зліва від точки М на відстані 2 см)
KY=18 см
DY=10 см
2) MY=18 см
KY=2 см ( точка Y лежить зправа від точки К на відстані 2 см)
DY=10 см
216 см²
Объяснение:
Дано: АВСD - трапеция, ВD⊥АВ, АС⊥СD, ВС=10 см, АD=26 см.
Доказать, что АВ=СD. Найти S(АВСD).
По условию ∠АВD=∠АСD=90°; значит, эти углы опираются на диаметр АD окружности, которую можно описать вокруг трапеции АВСD. Поскольку окружность можно описать только вокруг равнобедренной трапеции, то трапеция АВСD - равнобедренная.
Чтобы найти площадь трапеции, проведем высоты ВН и СК. Тогда
ВС=КН=10 см, АН=КD=(26-10):2=8 см.
Найдем СК из ΔАСD, где СК=√(АК*КD)=√((10+8)*8)=√144=12 см.
S=(ВС+АD):2*СК=36:2*12=216 см²