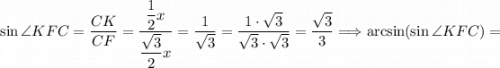Всего выделяют три основные группы минеральных удобрений:
Калийные. Группа минеральных удобрений, в состав которых входят соли с ионами калия (K⁺). Калий является крайне важным элементом в жизни растений, так как он участвует в синтезе органических веществ в клетках, регулирует водный обмен, повышает иммунитет растения, входит в состав клеточных мембран, является катализатором. Основные соли калия - хлорид калия KCl, сульфат калия K₂SO₄ и нитрат калия KNO₃.Фосфорные. Группа минеральных удобрений, в состав которых входят соли с ионами фосфора (P). Фосфор входит в состав некоторых белков и липидов, а соответственно участвует в образовании клеточных мембран, обеспечивает нормальное развитие побегов, корней и плодов, входит в состав ферментов, участвует в образовании АТФ при синтезе энергии. Основные соли из группы удобрений - дигидроортофосфат кальция Ca(H₂PO₄)₂, дигидрофосфат аммония NH₄H₂PO₄, гидрофосфат аммония (NH₄)₂HPO₄, ортофосфорная кислота H₃PO₄.Азотные. Группа минеральных удобрений, в состав которых входят соли с ионами азота (N). Азот участвует в синтезе АТФ (в составе аденина), обеспечивает развитие корневой системы и побегов, входит в состав всех белков, входит в состав хлорофилла (обеспечивает фотосинтез). Основные соли из группы удобрений - сульфат аммония (NH₄)₂SO₄, хлорид аммония NH₄Cl, сульфид аммония (NH₄)₂S, нитрат аммония NH₄NO₃.
Дано: ABCD - тетраэдр, AC = BC = AB = DA = DB = DC, ABK ⊥ CD
Найти: ∠(ABC, ABK) - ?
Решение: Пусть BD = x. Так как по условию AC = BC = AB = DA =
= DB = DC, то x = AC = BC = AB = DA = DB = DC. Проведем из точки K перпендикуляр к прямой AB в точку F. Так как точки A,B ∈ ABC и A,B ∈ ABK, то ABC ∩ ABK = AB.
Так как (F ∈ AB, ABC ∩ ABK= AB ⇒ AB ⊂ ABK) ⇒ F ∈ ABK, то KF ⊂ ABK.
Так как по условию ABK ⊥ CD, то по определению перпендикулярности прямой плоскости, прямая перпендикулярная плоскости, перпендикулярна любой прямой лежащей в этой плоскости, тогда KF ⊥ CD, так как KF ⊂ ABK. Так как KF ⊥ CD и KF ⊥ AB по построению, то по теореме о трех перпендикулярах CF ⊥ AB.
Так как CF ⊥ AB и KF ⊥ AB, то угол ∠KFC является линейным углом двухгранного угла ∠(ABC, ABK), то есть ∠(ABC, ABK) = ∠KFC.
Так как по условию AC = BC = AB = DA = DB = DC, то тетраэдр ABCD - правильный по определению. По свойствам правильного тетраэдра все его грани правильные треугольники, тогда треугольник ΔABC - правильный. По свойствам правильного треугольника все его углы равны 60°, тогда ∠CAB = 60°. Рассмотрим треугольник ΔCAF. Так как CF ⊥ AB, то треугольник ΔCAF - прямоугольный. . Так как CF ⊥ AB, то CF - высота правильного треугольника ΔABC. По свойствам правильного треугольника все его высоты являются медианами и биссектрисами, тогда точка F - середина отрезка AB. Так как все грани правильного тетраэдра правильные треугольники, то треугольник ΔADB - правильный. Проведем отрезок DF в треугольнике ΔΔADB. Так как точка F - середина отрезка AB, то отрезок DF - медиана, а по свойствам правильного треугольника биссектриса и высота. Так как по свойствам правильного тетраэдра(ABCD) все его грани равны между собой треугольник, то соответствующие элементы треугольников равны, тогда CF = DF как высоты правильных треугольников, следовательно треугольник ΔCFD - равнобедренный с основанием CD. Так как FK ⊥ CD, то по теореме высота равнобедренного треугольника проведенная к основанию(CD) является медианой и биссектрисой, то есть
Всего выделяют три основные группы минеральных удобрений:
Калийные. Группа минеральных удобрений, в состав которых входят соли с ионами калия (K⁺). Калий является крайне важным элементом в жизни растений, так как он участвует в синтезе органических веществ в клетках, регулирует водный обмен, повышает иммунитет растения, входит в состав клеточных мембран, является катализатором. Основные соли калия - хлорид калия KCl, сульфат калия K₂SO₄ и нитрат калия KNO₃.Фосфорные. Группа минеральных удобрений, в состав которых входят соли с ионами фосфора (P). Фосфор входит в состав некоторых белков и липидов, а соответственно участвует в образовании клеточных мембран, обеспечивает нормальное развитие побегов, корней и плодов, входит в состав ферментов, участвует в образовании АТФ при синтезе энергии. Основные соли из группы удобрений - дигидроортофосфат кальция Ca(H₂PO₄)₂, дигидрофосфат аммония NH₄H₂PO₄, гидрофосфат аммония (NH₄)₂HPO₄, ортофосфорная кислота H₃PO₄.Азотные. Группа минеральных удобрений, в состав которых входят соли с ионами азота (N). Азот участвует в синтезе АТФ (в составе аденина), обеспечивает развитие корневой системы и побегов, входит в состав всех белков, входит в состав хлорофилла (обеспечивает фотосинтез). Основные соли из группы удобрений - сульфат аммония (NH₄)₂SO₄, хлорид аммония NH₄Cl, сульфид аммония (NH₄)₂S, нитрат аммония NH₄NO₃.Объяснение:
Дано: ABCD - тетраэдр, AC = BC = AB = DA = DB = DC, ABK ⊥ CD
Найти: ∠(ABC, ABK) - ?
Решение: Пусть BD = x. Так как по условию AC = BC = AB = DA =
= DB = DC, то x = AC = BC = AB = DA = DB = DC. Проведем из точки K перпендикуляр к прямой AB в точку F. Так как точки A,B ∈ ABC и A,B ∈ ABK, то ABC ∩ ABK = AB.
Так как (F ∈ AB, ABC ∩ ABK= AB ⇒ AB ⊂ ABK) ⇒ F ∈ ABK, то KF ⊂ ABK.
Так как по условию ABK ⊥ CD, то по определению перпендикулярности прямой плоскости, прямая перпендикулярная плоскости, перпендикулярна любой прямой лежащей в этой плоскости, тогда KF ⊥ CD, так как KF ⊂ ABK. Так как KF ⊥ CD и KF ⊥ AB по построению, то по теореме о трех перпендикулярах CF ⊥ AB.
Так как CF ⊥ AB и KF ⊥ AB, то угол ∠KFC является линейным углом двухгранного угла ∠(ABC, ABK), то есть ∠(ABC, ABK) = ∠KFC.
Так как по условию AC = BC = AB = DA = DB = DC, то тетраэдр ABCD - правильный по определению. По свойствам правильного тетраэдра все его грани правильные треугольники, тогда треугольник ΔABC - правильный. По свойствам правильного треугольника все его углы равны 60°, тогда ∠CAB = 60°. Рассмотрим треугольник ΔCAF. Так как CF ⊥ AB, то треугольник ΔCAF - прямоугольный.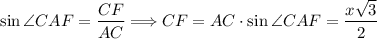
. Так как CF ⊥ AB, то CF - высота правильного треугольника ΔABC. По свойствам правильного треугольника все его высоты являются медианами и биссектрисами, тогда точка F - середина отрезка AB. Так как все грани правильного тетраэдра правильные треугольники, то треугольник ΔADB - правильный. Проведем отрезок DF в треугольнике ΔΔADB. Так как точка F - середина отрезка AB, то отрезок DF - медиана, а по свойствам правильного треугольника биссектриса и высота. Так как по свойствам правильного тетраэдра(ABCD) все его грани равны между собой треугольник, то соответствующие элементы треугольников равны, тогда CF = DF как высоты правильных треугольников, следовательно треугольник ΔCFD - равнобедренный с основанием CD. Так как FK ⊥ CD, то по теореме высота равнобедренного треугольника проведенная к основанию(CD) является медианой и биссектрисой, то есть
CK = KD = CD : 2 = x : 2 = 0,5x.
Рассмотрим прямоугольный треугольник ΔCKF.