Прямоугольный треугольник с катетами 3 и 4 - египетский, его гипотенуза 5 ( проверьте по т.Пифагора).
Проекция ВС наклонной В1С перпендикулярна СА. По т. о 3-х перпендикулярах В1С⊥СА. Треугольник В1СА - прямоугольный с углом В1АС=60°. В1С=АС•tg60°=4√3. Т.к. призма прямая, боковые ребра перпендикулярны основаниям, поэтому треугольник В1ВС прямоугольный. По т. Пифагора В1В=√(B1C²-BC²)=√[(4√3)²-3²]=√39
Боковое ребро прямой призмы является её высотой, а её боковые грани - прямоугольники.
Площадь боковой поверхности призмы находят умножением её высоты на периметр основания.
ответ: 12√39 (ед. площади)
Объяснение:
Прямоугольный треугольник с катетами 3 и 4 - египетский, его гипотенуза 5 ( проверьте по т.Пифагора).
Проекция ВС наклонной В1С перпендикулярна СА. По т. о 3-х перпендикулярах В1С⊥СА. Треугольник В1СА - прямоугольный с углом В1АС=60°. В1С=АС•tg60°=4√3. Т.к. призма прямая, боковые ребра перпендикулярны основаниям, поэтому треугольник В1ВС прямоугольный. По т. Пифагора В1В=√(B1C²-BC²)=√[(4√3)²-3²]=√39
Боковое ребро прямой призмы является её высотой, а её боковые грани - прямоугольники.
Площадь боковой поверхности призмы находят умножением её высоты на периметр основания.
S(бок)=В1В•(АВ+ВС+АС)=√39•12=12√39 (ед. площади)
Sбок= Р*h Sбок=(АВ+ВС+СД ) * АА1
1) т.к угАСВ=90* по условию, и призма прямая, то двугранный угол АСС1В1 =90* . значт угА1СВ=90*
2) рассмотрим треуг А1СВ=прямоуг, угС=90*, СА1В=30*, А1В=10см,
СВ=А1В * sin30* CB=5cm
3) рассмотрим АВС-прямоуг, угС=90* АС=СВ=5см, т.е АВС равнобедренный
по тПифагора АВ= sqrt 2AC^2 AB=5sqrt2
4) рассмотрим АА1В- прямоугольный , угА=90, АВ=5sqrt2 , А1В=10
из тПифагора АА1=sqrt ( A1B^2 -AB^2) AA1=sqrt(100- 50)= 5sqrt2
5) Sбок = (5sqrt2 + 5 + 5 ) * 5 sqrt2 =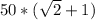 cm
cm