ГЕОМЕТРИЯ Даны координаты точек:
A(−5;7);
B(−2;5);
C(3;−3);
D(6;−5).
Докажи, что AB−→−=CD−→−, ответ приложи в виде файла.
2.Среди данных векторов укажи пары:
a. одинаково направленных векторов
(3;−5)
(12;−20)
(−20;−12)
(5;3)
б. противоположно направленных векторов
(−20;−12)
(3;−5)
(5;3)
(12;−20)
3. Даны координаты векторов a→ и b→.
Определи координаты векторов a→+b→ и b→−a→.
a→{12;6};
b→{−29;−1};
a→+b→{
;
};
b→−a→{
;
}.
4. Даны координаты векторов a→ и b→.
Определи координаты векторов a→+b→ и b→−a→.
a→{12;6};
b→{−29;−1};
a→+b→{
;
};
b→−a→{
;
}.
Найдем ВС. По свойству медианы, проведенной к гипотенузе, ВС=2АМ=15*2=30 см.
ВМ=СМ=30:2=15 см.
Из прямоугольного треугольника АМН найдем МН.
МН=√(АМ²-МН²)=√(225-144)=√81=9 см.
НС=МС-МН=15-9=6 см.
Из треугольника АНС найдем АС:
АС=√(АН²+СН²)=√(144+36)=√180=6√5 см.
Найдем АВ:
АВ²=ВС²-АС²=900-180=720; АВ=√720=12√5 см.
sin A=sin 90°=1
sin B=AC\BC=6√5\30=√5\5
sin C=AB\BC=12√5\30=2√5\5
ответы: 30 см; 6√5 см; 12√5 см; 1; √5\5; 2√5\5.
Дано:
ABCDA₁B₁C₁D₁ - прямая призма; ABCD - основание призмы, равнобедренная трапеция; AD - основание трапеции; BC = 5см; AD = 11см; AC = 10см; AC₁ = 26см.
*Все диагонали призмы равны между собой (BD₁=B₁D=AC₁=A₁C), поскольку призма прямая и в основании равнобедренная трапеция.
Найти:
V - ?
В трапеции ABCD:
опустим перпендикуляры BH₁ и CH₂;
BH₁⊥AD, BC║AD ⇒ BCH₂H₁ - прямоугольник;
BC = H₁H₂ = 5см, как противоположные стороны прямоугольника;
трапеция равнобедренная, поэтому AH₁ = H₂D;
AH₁ = (AD-H₁H₂):2 = (11-5):2 = 3 см;
AH₂ = AH₁+H₁H₂ = 3+5 = 8 см.
В прямоугольном ΔAH₂C (∠CH₂A=90°):
AC=10см; AH₂=8см;
По теореме Пифагора:
(CH₂)² = AC²-(AH₂)²;
(CH₂)² = 10²-8² = 100-64 = 6² см²;
CH₂ = 6см.
CC₁⊥(ABC) т.к. призма прямая; AC⊂(ABC);
Тогда CC₁⊥AC.
В прямоугольном ΔACC₁ (∠ACC₁=90°):
AC₁=26см; AC=10см;
По теореме Пифагора:
(CC₁)² = (AC₁)²-AC²;
(CC₁)² = 26²-10² = (26-10)(26+10) = 16·36 = (4·6)² см²;
CC₁ = 24см.
Объём призмы равен значению произведения её высоты и площади основания. Боковое ребро прямой призмы является также и высотой.Площадь трапеции равна значению произведения полусуммы оснований и высоты трапеции.V = CC₁·S(ABCD) =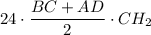
= 12·(5+11)·6 = 72·16 = 1152 см²
ответ: 1152см².