Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
Вариант 1.
1.
Для начала найдём один из отрезков, полученным, делением гипотенузы высотою: отрезок BD.
Так как это высота, то отрезок образует 2 прямых угла: <BDA; <ADC.
Тоесть образуется 2 прямоугольных треугольника: ΔBDA; ΔADC.
По теореме Пифагора — BC равен:
Чтобы найти всю гипотенузу BC — вычислим оставшийся отрезок DC.
Для этого нам нужна одна из формул вычисления высоты прямоугольного треугольника:
DC = 9; BD = 16 => BC = 9+16 = 25см.
По теореме Пифагора, AC равен:
Косинус угла равен отношению прилежащего катета к гипотенузе, то есть:
Вывод: AC = 21.9см; cos(<C) = 0.876.
2.
Для начала найдём оставшийся стороны паралеллограмма: BD & AD, которые друг другу равны.
Так как BD — перпендикулярен стороне AD — то он образует прямой угол с этой сторон, тоесть: ΔADB — прямоугольный.
Формула вычисления стороны BD, зная угол A, и гипотенузу AB: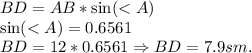
Осталось найти сторону AD (по теореме Пифагора), на которой проведена высота BD, чтобы потом найти площадь:
Теперь, формула вычисления площад параллелограмма такова: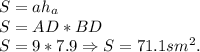
Вывод: S = 71.1см².