В правильную 4-х угольную усеченную пирамиду вписан куб так, что одна из граней куба совпадает с меньшим основанием усеченной пирамиды , а противоположная грань куба лежит на большем основании усеченной пирамиды . Ребро куба равно a , сторона меньшего основания усеченной пирамиды в 2 раза меньше стороны большего основания .Найдите площадь боковой поверхности усеченной пирамиды
Объяснение:
Т.к. одна из граней куба совпадает с меньшим основанием усеченной пирамиды, то сторона верхнего основания равна а ⇒ сторона большего основания усеченной пирамиды 2а.
Т.к. усеченная пирамида правильная , то боковые грани равнобедренные трапеции.
S( бок. усеч. пир.)=4S( трапеции)=4*1/2*h*(a+2a). Найдем высоту из прямоугольной трапеции ОО₁Р₁Р .
Точка О₁-точка пересечения диагоналей квадрата, поэтому О₁Р₁= Пусть Р₁К⊥ОР, тогда КР=а- =
В математике и теоретической физике зеркальной симметриейназывается Калаби — Яу в следующем смысле. Два многообразия Калаби — Яу могут быть совершенно разными геометрически, но давать одинаковую физику элементарных частиц при использовании их в качестве «свёрнутых» дополнительных размерностейтеории струн. Сами такие многообразия называют зеркально симметричными.
Зеркальная симметрия была изначально обнаружена физиками. Математики заинтересовались этим явлением около 1990 года, когда Филип Канделас, Ксения де ла Осса, Пол Грин и Линда Паркс показали, что зеркальную симметрию можно использовать в качестве инструмента в исчислительной геометрии, разделе математики, занимающемся подсчётом количества ответов на те или иные геометрические вопросы. Канделас и соавторы показали, что зеркальная симметрия может быть использована для подсчёта числа рационально квивых на многообразии Калаби — Яу, что решает долго не поддававшуюся задачу. Несмотря на то, что первоначальный подход к зеркальной симметрии базировался на идеях, сформулированных на физическом уровне строгости, математики смогли строго доказать некоторые из предсказаний, сделанные физиками.
В правильную 4-х угольную усеченную пирамиду вписан куб так, что одна из граней куба совпадает с меньшим основанием усеченной пирамиды , а противоположная грань куба лежит на большем основании усеченной пирамиды . Ребро куба равно a , сторона меньшего основания усеченной пирамиды в 2 раза меньше стороны большего основания .Найдите площадь боковой поверхности усеченной пирамиды
Объяснение:
Т.к. одна из граней куба совпадает с меньшим основанием усеченной пирамиды, то сторона верхнего основания равна а ⇒ сторона большего основания усеченной пирамиды 2а.
Т.к. усеченная пирамида правильная , то боковые грани равнобедренные трапеции.
S( бок. усеч. пир.)=4S( трапеции)=4*1/2*h*(a+2a). Найдем высоту из прямоугольной трапеции ОО₁Р₁Р .
Точка О₁-точка пересечения диагоналей квадрата, поэтому О₁Р₁=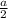
Пусть Р₁К⊥ОР, тогда КР=а- 
=
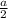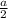
Из ΔКРР₁ по т. Пифагора Р₁К=√(а²+(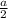
)²)=а√
=
.
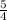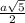S( бок. усеч. пир.)=4*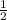
*
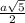*(a+2a)=3a²√5 (ед²).
Зеркальная симметрия была изначально обнаружена физиками. Математики заинтересовались этим явлением около 1990 года, когда Филип Канделас, Ксения де ла Осса, Пол Грин и Линда Паркс показали, что зеркальную симметрию можно использовать в качестве инструмента в исчислительной геометрии, разделе математики, занимающемся подсчётом количества ответов на те или иные геометрические вопросы. Канделас и соавторы показали, что зеркальная симметрия может быть использована для подсчёта числа рационально квивых на многообразии Калаби — Яу, что решает долго не поддававшуюся задачу. Несмотря на то, что первоначальный подход к зеркальной симметрии базировался на идеях, сформулированных на физическом уровне строгости, математики смогли строго доказать некоторые из предсказаний, сделанные физиками.