если не трудно начертите рисунок, а то не пойму какой. Через внешнюю точку Е окружности проведены две прямые, пересекающие окружность соответственно в точках А, С и В, D. Докажите, что треугольники ADЕ и BCЕ подобны.​

Дано:

усеченный конус

r = O₁B = 5 см

R = OA = 11 см

см

-----------------------------

Найти:

Sсеч - ?

1) Проведем BH⊥AO.

  OH = O₁B = r = 5 см

  AH = OA - OH = R - r = 11 см - 5 см = 6 см

2) Рассмотрим ΔAHB:

   BH⊥AO        |  ⇒ ΔAHB - прямоугольный

   ∠AHB = 90° |

   AB² = AH² + HB² - по теореме Пифагора, следовательно: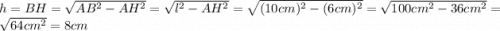h = BH = OO₁ = 8 см

3) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса: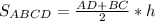

4) В трапеции ABCD:

   AD = 2AO = 2R = 2×11 см = 22 см      h = BH= 8 см

   BC = 2BO₁ = 2r = 2×5 см = 10 см

5) Тогда площадь трапеции равна:

⇒

Sсеч =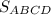 = 128 см²

ответ: Sсеч = 128 см²

P.S. Рисунок показан внизу↓

На рисунке изображена прямоугольная трапеция ABCD, в которую вписан круг. Точка касания окружности делит большую боковую сторону на отрезки длиной 4 см и 25 см. Установите соответствие между началом предложения (1 - 4) и его окончанием (а-д) так, чтобы образовалось правильное утверждение

1 Средняя линия трапеции равна ,2 Высота трапеции равна , 3 радиус вписанной окружности равен , 4 Меньшая диагональ трапеции равна

A )√ 594 см , Б) 20 см, В)2√149 см , Г) 10 см , Д) 24,5 см

Объяснение:

1) Найдем радиус вписанной окружности r=√(CH*HD)=√(4*25)10 (cм)⇒

диаметр ,равный высоте трапеции , равен 2*10=20( см), h=20 cм.

2)Высота прямоугольной трапеции равна меньшей боковой стороне ⇒ АВ=20 см.

3)Суммы противоположных сторон любого четырёхугольника описанного около окружности равны :  АВ+CD=BC+AD ⇒BC+AD=20+29=49 (см)

По определению средней линии трапеции имеем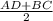  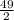 = =24,5(см)

4) Меньшей диагональю будет АС.

По свойству отрезков касательных СН=СК=4 см, ВМ=ВК=10 см, тогда ВС=4+10=14 (см)

ΔАВС-прямоугольный по т. Пифагора АС=√(14²+20²)=√596=√(4*149)=2√149 ( см).

ответ .   1-Д   ; 2-Б    ; 3-Г  ; 4-В .