Такую задачу можно делать с теоремы о пропорциональных отрезках, но при этом нужно проводить дополнительные линии, а мне делать это лень. Поэтому воспользуемся теоремой Менелая. Советую перед разбором решения ознакомиться с формулировкой этой теоремы. А заодно и с теоремой Чевы. А если посмотрите и теорему Ван-Обеля, вы будете подкованы на 100%.
Кстати, удобно сначала воспользоваться теоремой Чевы. Поскольку чевианы PM, RK и QN пересекаются в одной точке, справедливо равенство.
То есть в QK четыре части, а в KP одна часть. Следовательно, в PQ=PK+KQ пять частей, а тогда
Для нахождения второго отношения воспользуемся теоремой Ван-Обеля. Поскольку чевианы PM, RK и QN пересекаются в точке S, то
Для нахождения третьего отношения применим теорему Менелая к треугольнику PRS и прямой NK, которая пересекает стороны PR и PS и продолжение стороны RS. Имеем:
Внимание для тех, кто хочет (и знает, как) сделать сайт лучше и комфортнее! В данный момент я имею в виду не преодоление тех очевидных недостатков, которые становятся очевидными в первые пять минут, а плохую работу встроенного TEX'а. Впечатление, что здешние айтишники не знают, как решить возникающие проблемы. Предложите им свои услуги!
Продолжим боковые стороны до точки пересечения T. (Выходит что BC средняя линия треугольника ATD) Проведем FO||AT ,OL||TD. Откуда подобны треугольники: ATD и FOL,AMD и FOD,AND и AOL. Откуда верны отношения: FO/4y=LO/6z=FL/AD FO/y=(FL+LD)/AD=OD/MD; FO/4y=(FL+LD)/4AD LO/2z=(FL+AF)/AD ; LO/6z=(FL+AF)/3AD (FL+LD)/4AD=FL/AD FL+LD=4FL LD=3FL (FL+AF)/3AD=FL/AD FL+AF=3FL AF=2FL OD/MD=(FL+LD)/(AF+FL+LD)=4FL/(6FL)=2/3 Проведем диагональ BD. Треугольники ABD и BDC имеют одинаковые высоты, равные высоте трапеции. То есть их площади относятся как основы трапеции: SBCD=SABD/2 (в сумме они дают площадь трапеции) 27cм^2=SABD+SABD/2=3SABD/2 SABD=18cм^2 Треугольники ABD и AMD имеют общую высоту,то их площади тоже относятся как их основы (AM и AB): SAMD=SABD/2=9cм^2 Ну и наконец треугольники AMD и AOD тоже имеют общую высоты,то их площади тоже относятся как основы (OD и MD). Из выше показанного:OD/MD=2/3 Откуда: SAOD=2SAMD/3=18/3=6cм^2 ответ:SAOD=6cм^2 Я не гарантирую ,что это самый простой путь решения. Я даже на 100 процентов уверен,что есть попроще.
Такую задачу можно делать с теоремы о пропорциональных отрезках, но при этом нужно проводить дополнительные линии, а мне делать это лень. Поэтому воспользуемся теоремой Менелая. Советую перед разбором решения ознакомиться с формулировкой этой теоремы. А заодно и с теоремой Чевы. А если посмотрите и теорему Ван-Обеля, вы будете подкованы на 100%.
Кстати, удобно сначала воспользоваться теоремой Чевы. Поскольку чевианы PM, RK и QN пересекаются в одной точке, справедливо равенство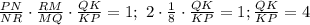 .
.
То есть в QK четыре части, а в KP одна часть. Следовательно, в PQ=PK+KQ пять частей, а тогда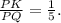
Для нахождения второго отношения воспользуемся теоремой Ван-Обеля. Поскольку чевианы PM, RK и QN пересекаются в точке S, то
Для нахождения третьего отношения применим теорему Менелая к треугольнику PRS и прямой NK, которая пересекает стороны PR и PS и продолжение стороны RS. Имеем:
Внимание для тех, кто хочет (и знает, как) сделать сайт лучше и комфортнее! В данный момент я имею в виду не преодоление тех очевидных недостатков, которые становятся очевидными в первые пять минут, а плохую работу встроенного TEX'а. Впечатление, что здешние айтишники не знают, как решить возникающие проблемы. Предложите им свои услуги!
Проведем FO||AT ,OL||TD. Откуда подобны треугольники:
ATD и FOL,AMD и FOD,AND и AOL.
Откуда верны отношения:
FO/4y=LO/6z=FL/AD
FO/y=(FL+LD)/AD=OD/MD; FO/4y=(FL+LD)/4AD
LO/2z=(FL+AF)/AD ; LO/6z=(FL+AF)/3AD
(FL+LD)/4AD=FL/AD
FL+LD=4FL
LD=3FL
(FL+AF)/3AD=FL/AD
FL+AF=3FL
AF=2FL
OD/MD=(FL+LD)/(AF+FL+LD)=4FL/(6FL)=2/3
Проведем диагональ BD.
Треугольники ABD и BDC имеют одинаковые высоты, равные высоте трапеции. То есть их площади относятся как основы трапеции:
SBCD=SABD/2 (в сумме они дают площадь трапеции)
27cм^2=SABD+SABD/2=3SABD/2
SABD=18cм^2
Треугольники ABD и AMD имеют общую высоту,то их площади тоже относятся как их основы (AM и AB):
SAMD=SABD/2=9cм^2
Ну и наконец треугольники AMD и AOD тоже имеют общую высоты,то их площади тоже относятся как основы (OD и MD).
Из выше показанного:OD/MD=2/3
Откуда: SAOD=2SAMD/3=18/3=6cм^2
ответ:SAOD=6cм^2
Я не гарантирую ,что это самый простой путь решения.
Я даже на 100 процентов уверен,что есть попроще.