ΔTRS- равнобедренный, так как RТ=ТS, а высота, проведённая к основанию равнобедренного треугольника является его медианой, следовательно RЕ=ЕS=RS:2=24:2=12(см)
ΔTЕS- прямоугольный, следовательно по теореме Пифагора
TS²=ТЕ²+ЕS²=8²+12²=64+144=208
(см),
RT²=208
По теореме косинусов в ΔTRS
TS²= RТ² +RS² -2TR*RS* соs∠ R ;
2RТ*RS соs∠ R = RТ² +RS²- TS²; ( так как RТ=ТS, то RТ²-ТS²=0)
1. Зная сумму углов треугольника, находим угол В: <B=180-<C-<A=180-90-60=30° Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Значит АС=АВ/2 По условию АС+АВ=26,4. Подставим сюда значение АС и запишем: АВ/2+АВ=26,4 3АВ/2=26,4 3АВ=52,8 АВ=17,6 см
2. Зная внешний угол, находим внутренний угол А треугольника АВС: <A=180-120=60° <B=180-<C-<A=180-90-60=30° Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Значит АС=АВ/2 По условию АС+АВ=18. Подставив сюда значение АС, запишем: АВ/2+АВ=18 3АВ/2=18 3АВ=36 АВ=12 см Как было указано выше, АС=АВ/2, значит АС=12/2=6 см
3. Поскольку треугольник равносторонний, все углы в нем по 60°. Рассмотрим прямоугольный треугольник DMC. Здесь DC=BC/2=12/2=6 см cos C=CM/DC, отсюда СМ=cos C*DC=cos 60 * 6=1/2 * 6 = 3 см АМ=АС-СМ=12-3=9 см
ответ: TS=4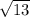
ΔTRS- равнобедренный, так как RТ=ТS, а высота, проведённая к основанию равнобедренного треугольника является его медианой, следовательно RЕ=ЕS=RS:2=24:2=12(см)
ΔTЕS- прямоугольный, следовательно по теореме Пифагора
TS²=ТЕ²+ЕS²=8²+12²=64+144=208
RT²=208
По теореме косинусов в ΔTRS
TS²= RТ² +RS² -2TR*RS* соs∠ R ;
2RТ*RS соs∠ R = RТ² +RS²- TS²; ( так как RТ=ТS, то RТ²-ТS²=0)
2RT*RS *соs ∠R =RS²;
RT*RS соs ∠R =RS²/2
В ΔRKS : RK=RT/2.
По теореме косинусов
SK²=RK²+RS²-2RK*RS*cos∠R=(RT/2)²+RS²-2(RT/2)*RS* соs ∠R=
=TR²/4+RS²- RT*RS* соs ∠R =TR²/4+RS² - RS²/2=
<B=180-<C-<A=180-90-60=30°
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Значит
АС=АВ/2
По условию АС+АВ=26,4. Подставим сюда значение АС и запишем:
АВ/2+АВ=26,4
3АВ/2=26,4
3АВ=52,8
АВ=17,6 см
2. Зная внешний угол, находим внутренний угол А треугольника АВС:
<A=180-120=60°
<B=180-<C-<A=180-90-60=30°
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Значит
АС=АВ/2
По условию АС+АВ=18. Подставив сюда значение АС, запишем:
АВ/2+АВ=18
3АВ/2=18
3АВ=36
АВ=12 см
Как было указано выше, АС=АВ/2, значит АС=12/2=6 см
3. Поскольку треугольник равносторонний, все углы в нем по 60°. Рассмотрим прямоугольный треугольник DMC. Здесь DC=BC/2=12/2=6 см
cos C=CM/DC, отсюда
СМ=cos C*DC=cos 60 * 6=1/2 * 6 = 3 см
АМ=АС-СМ=12-3=9 см