Рассмотрим произвольный треугольник ABC, в котором AH является как медианой, так и высотой. Докажем, что он является равнобедренным.
I)В нём этот отрезок будет являться частью срединного перпендикуляра к стороне BC, поэтому по теореме о срединном перпендикуляра к отрезку, AB=AC как расстояния от точки A, лежащей на нём до точек B и C, т.е. треугольник ABC является равнобедренным по определению, что и требовалось доказать.
II)Высота разделяет этот треугольник на два прямоугольных: HAB и HAC. Они равны по двум катетам: катет AH - общий, катеты BH и CH равны как отрезки, на которые медиана делит противоположную сторону. Из равенства этих треугольников следует и равенство их 1) соответственных углов: <ABC=<ACB, поэтому рассматриваемый треугольник является равнобедренным по признаку равнобедренного треугольника, что и требовалось доказать; 2) соответственных сторон: AB=AC, поэтому рассм. тр. является равноб. по определению, что и требовалось доказать.
III)В рассматриваемом треугольнике в прямоугольных треугольниках HAB и HAC по теореме Пифагора и , Но по условию BH=CH, поэтому AB=AC, т.е. рассм. тр. - равноб. по определению, ч. т. д.
Когда медиана совпадает с высотой в треугольнике, высота перпендикулярна основанию и отрезки, на которые делится основание равны.
Докажем, что треугольники, на которые делится большой тр-к равны между собой.
Нижние катеты равны по условию (медиана), высота - общая, и углы прямые.
Треугольники равны по двум сторонам и углу между ними.
В равных треугольниках соответствующие стороны равны, значит равны и боковые стороны - треугольник равнобедренный.
Рассмотрим произвольный треугольник ABC, в котором AH является как медианой, так и высотой. Докажем, что он является равнобедренным.
I)В нём этот отрезок будет являться частью срединного перпендикуляра к стороне BC, поэтому по теореме о срединном перпендикуляра к отрезку, AB=AC как расстояния от точки A, лежащей на нём до точек B и C, т.е. треугольник ABC является равнобедренным по определению, что и требовалось доказать.
II)Высота разделяет этот треугольник на два прямоугольных: HAB и HAC. Они равны по двум катетам: катет AH - общий, катеты BH и CH равны как отрезки, на которые медиана делит противоположную сторону. Из равенства этих треугольников следует и равенство их 1) соответственных углов: <ABC=<ACB, поэтому рассматриваемый треугольник является равнобедренным по признаку равнобедренного треугольника, что и требовалось доказать; 2) соответственных сторон: AB=AC, поэтому рассм. тр. является равноб. по определению, что и требовалось доказать.
III)В рассматриваемом треугольнике в прямоугольных треугольниках HAB и HAC по теореме Пифагора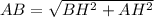 и
и 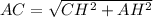 , Но по условию BH=CH, поэтому AB=AC, т.е. рассм. тр. - равноб. по определению, ч. т. д.
, Но по условию BH=CH, поэтому AB=AC, т.е. рассм. тр. - равноб. по определению, ч. т. д.