Войти Регистрация Спроси ai-bota

Докажите, что четырехугольник с вершинами е(-2 ; 0), f(2; 2), м(4; -2) и n(0; -4) является квадратом

Показать ответ

Ответ:

Ynushkevich333

11.06.2020 19:26

Вектор EF имеет координаты (2-(-2); 2-0) = (4; 2). Его длина
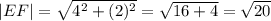
$|EF|=\sqrt{4^2+(2)^2}=\sqrt{16+4}=\sqrt{20}\\$
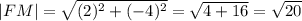
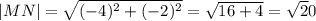
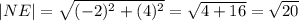
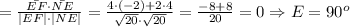
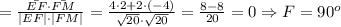
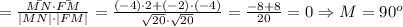
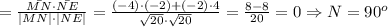
Вектор FM имеет координаты (4-2; -2-2) = (2; -4). Его длина
$|FM|=\sqrt{(2)^2+(-4)^2}=\sqrt{4+16}=\sqrt{20}$
Вектор MN имеет координаты (0-4; -4-(-2)) = (-4; -2). Его длина
$|MN|=\sqrt{(-4)^2+(-2)^2}=\sqrt{16+4}=\sqrt20$
Вектор NE имеет кооординаты (-2-0; 0-(-4)) = (-2; 4). Его длина
$|NE|=\sqrt{(-2)^2+(4)^2}=\sqrt{4+16}=\sqrt{20}$
Все стороны четырёхугольника равны. Найдём углы между ними:
$\cosE=\frac{\bar{EF}\cdot\bar{NE}}{|EF|\cdot|NE|}=\frac{4\cdot(-2)+2\cdot4}{\sqrt{20}\cdot\sqrt{20}}=\frac{-8+8}{20}=0\Rightarrow E=90^o$
$\cosF=\frac{\bar{EF}\cdot\bar{FM}}{|EF|\cdot|FM|}=\frac{4\cdot2+2\cdot(-4)}{\sqrt{20}\cdot\sqrt{20}}=\frac{8-8}{20}=0\Rightarrow F=90^o$
$\cosM=\frac{\bar{MN}\cdot\bar{FM}}{|MN|\cdot|FM|}=\frac{(-4)\cdot2+(-2)\cdot(-4)}{\sqrt{20}\cdot\sqrt{20}}=\frac{-8+8}{20}=0\Rightarrow M=90^o$
$\cosN=\frac{\bar{MN}\cdot\bar{NE}}{|MN|\cdot|NE|}=\frac{(-4)\cdot(-2)+(-2)\cdot4}{\sqrt{20}\cdot\sqrt{20}}=\frac{8-8}{20}=0\Rightarrow N=90^o$
Все стороны равны, угол между сторонами прямой. Значит, EFMN - квадрат.

0,0(0 оценок)

Популярные вопросы: Геометрия

adilyabaxtigar

31.05.2023 06:32

гострий кут ромба дорівнює 60 градусів знайдіть кути між діагоналями ромба і його сторонами. Буду благодарен, за схему....

alexnn08

27.10.2022 23:06

Здравствуйте Желательно подробное решение. Задана афинная система координат. Длина первого базисного вектора 2√3 , длина второго базисного вектора 1; угол между векторами...

Jasurka940

03.06.2021 23:56

Постройте угол косинус которого равен 3/9 ; 2/5...

lisya778

20.11.2020 20:15

Точки и лежат на одной прямой, точка не лежит на этой прямой, но находится на одинаковых расстояниях от точек и . Величина угла ∡α = 147°. Определи: 1. вид треугольника...

hcggchhcfuj

13.09.2022 07:45

Дві сторони трикутника дорівнюють 6 см і 8 см, а медіана, проведена до третьої сторони, дорівнює Знайдіть третю сторону трикутника...

jullii55

13.02.2022 20:05

Знайди відношення чисел 28 до 7...

tatiana2017D

16.05.2021 10:28

оченьДана функция y=−t+2. При каких значениях t значение функции равно −4?...

yoongi2017

09.11.2022 22:24

ТОЛЬКО очень над ,я на вас надеюсь...

Ьрнрг

27.09.2020 02:04

ВК — висота рівнобедреного трикутника АВС з основою АС. Знайдіть АС, якщо АВ = 12 см, ∠В = 60°...

di1808

01.01.2022 07:39

По данным рисунка найдите площадь треугольника ABC...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку