Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их и
Проведём диагональ в квадрате и диагональ в квадрате
Рассмотрим .
У квадрата все углы прямые.
, по свойству квадрата.
, так как диагонали квадрата делят углы пополам.
по 1 признаку подобия треугольников.
4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
В пятиугольнике сумма углов равна (5-2)*180=540°
Значит остальные углы, кроме А равны (540-60)/4=120°
Продолжим линии AB и СD до точки пересечения F. И продолжим линии EA и CD до точки пересечения G.
Угол FBС=180-120=60°
Угол FCB=180-120=60°
Угол F=180-(60+60)=60°
Угол G=180-(60+60)=60°
Следовательно треугольник AFG - равносторонний. А так же треугольники FBC и GED тоже равносторонние.
Обозначим неизвестные части сторон x и у.
6+x=7+y=4+x+y
6+x=4+x+y
y=2
7+y=7+2=9см - сторона треугольника АFG.
Расстояние от А до CD - высота треугольника АFG, которая равна (9/2)*√3=4,5√3см
ответ: 4,5√3см.
Всё в разделе "Объяснение".
Объяснение:1. Неверно.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их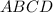 и
и 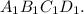
Проведём диагональ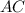 в квадрате
в квадрате 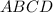 и диагональ
и диагональ 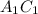 в квадрате
в квадрате 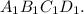
Рассмотрим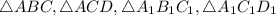 .
.
У квадрата все углы прямые.4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.